RobustPeriod: Time-Frequency Mining for Robust Multiple Periodicities Detection

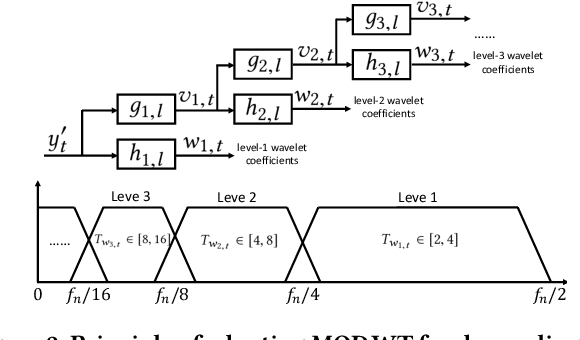
Periodicity detection is an important task in time series analysis as it plays a crucial role in many time series tasks such as classification, clustering, compression, anomaly detection, and forecasting. It is challenging due to the following reasons: 1, complicated non-stationary time series; 2, dynamic and complicated periodic patterns, including multiple interlaced periodic components; 3, outliers and noises. In this paper, we propose a robust periodicity detection algorithm to address these challenges. Our algorithm applies maximal overlap discrete wavelet transform to transform the time series into multiple temporal-frequency scales such that different periodicities can be isolated. We rank them by wavelet variance and then at each scale, and then propose Huber-periodogram by formulating the periodogram as the solution to M-estimator for introducing robustness. We rigorously prove the theoretical properties of Huber-periodogram and justify the use of Fisher's test on Huber-periodogram for periodicity detection. To further refine the detected periods, we compute unbiased autocorrelation function based on Wiener-Khinchin theorem from Huber-periodogram for improved robustness and efficiency. Experiments on synthetic and real-world datasets show that our algorithm outperforms other popular ones for both single and multiple periodicity detection. It is now implemented and provided as a public online service at Alibaba Group and has been used extensive in different business lines.