Robust Training of Neural Networks at Arbitrary Precision and Sparsity
Paper and Code
Sep 14, 2024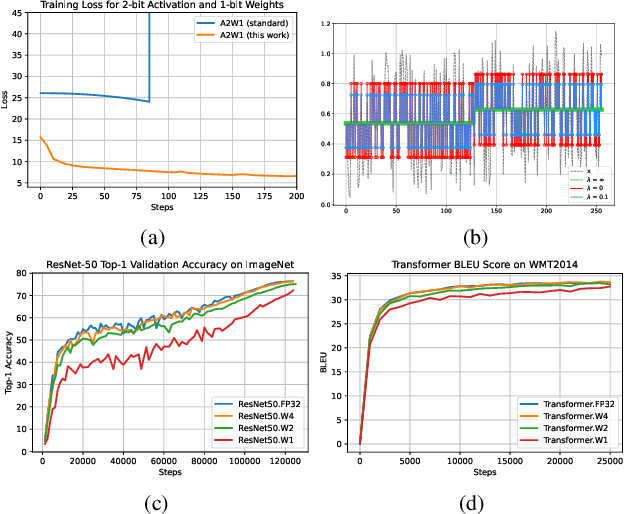
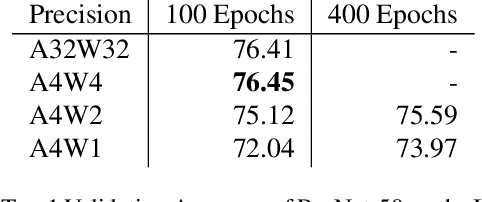

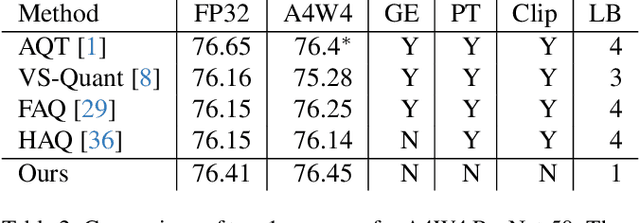
The discontinuous operations inherent in quantization and sparsification introduce obstacles to backpropagation. This is particularly challenging when training deep neural networks in ultra-low precision and sparse regimes. We propose a novel, robust, and universal solution: a denoising affine transform that stabilizes training under these challenging conditions. By formulating quantization and sparsification as perturbations during training, we derive a perturbation-resilient approach based on ridge regression. Our solution employs a piecewise constant backbone model to ensure a performance lower bound and features an inherent noise reduction mechanism to mitigate perturbation-induced corruption. This formulation allows existing models to be trained at arbitrarily low precision and sparsity levels with off-the-shelf recipes. Furthermore, our method provides a novel perspective on training temporal binary neural networks, contributing to ongoing efforts to narrow the gap between artificial and biological neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge