Robust and Recursively Feasible Real-Time Trajectory Planning in Unknown Environments
Paper and Code
Jul 14, 2021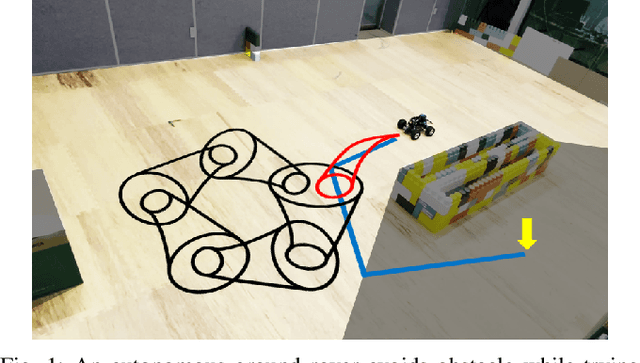
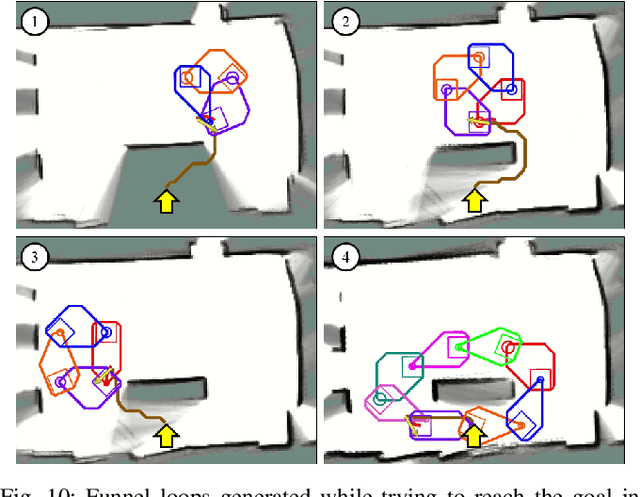


Motion planners for mobile robots in unknown environments face the challenge of simultaneously maintaining both robustness against unmodeled uncertainties and persistent feasibility of the trajectory-finding problem. That is, while dealing with uncertainties, a motion planner must update its trajectory, adapting to the newly revealed environment in real-time; failing to do so may involve unsafe circumstances. Many existing planning algorithms guarantee these by maintaining the clearance needed to perform an emergency brake, which is itself a robust and persistently feasible maneuver. However, such maneuvers are not applicable for systems in which braking is impossible or risky, such as fixed-wing aircraft. To that end, we propose a real-time robust planner that recursively guarantees persistent feasibility without any need of braking. The planner ensures robustness against bounded uncertainties and persistent feasibility by constructing a loop of sequentially composed funnels, starting from the receding horizon local trajectory's forward reachable set. We implement the proposed algorithm for a robotic car tracking a speed-fixed reference trajectory. The experiment results show that the proposed algorithm can be run at faster than 16 Hz, while successfully keeping the system away from entering any dead-end, to maintain safety and feasibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge