Robots with Attitude: Singularity-Free Quaternion-Based Model-Predictive Control for Agile Legged Robots
Paper and Code
Sep 17, 2024
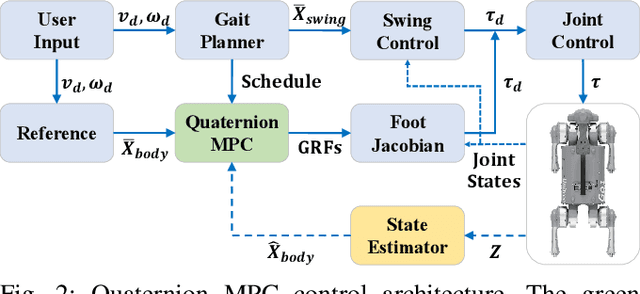
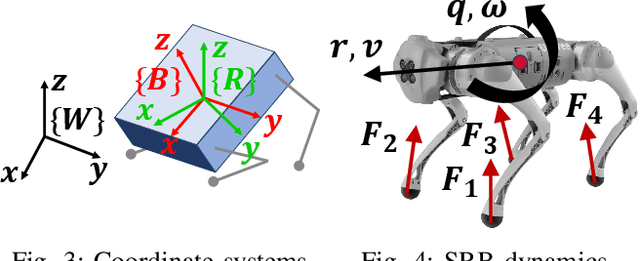
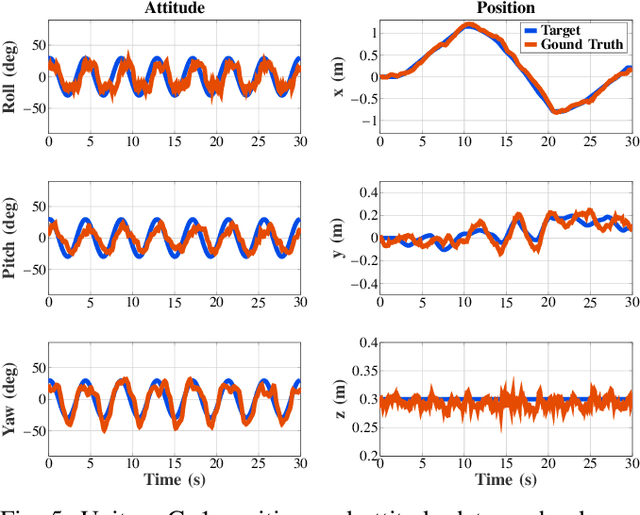
We present a model-predictive control (MPC) framework for legged robots that avoids the singularities associated with common three-parameter attitude representations like Euler angles during large-angle rotations. Our method parameterizes the robot's attitude with singularity-free unit quaternions and makes modifications to the iterative linear-quadratic regulator (iLQR) algorithm to deal with the resulting geometry. The derivation of our algorithm requires only elementary calculus and linear algebra, deliberately avoiding the abstraction and notation of Lie groups. We demonstrate the performance and computational efficiency of quaternion MPC in several experiments on quadruped and humanoid robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge