Revisiting Optimal Convergence Rate for Smooth and Non-convex Stochastic Decentralized Optimization
Paper and Code
Oct 14, 2022
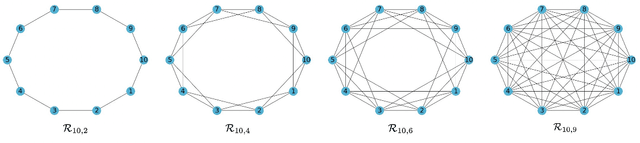

Decentralized optimization is effective to save communication in large-scale machine learning. Although numerous algorithms have been proposed with theoretical guarantees and empirical successes, the performance limits in decentralized optimization, especially the influence of network topology and its associated weight matrix on the optimal convergence rate, have not been fully understood. While (Lu and Sa, 2021) have recently provided an optimal rate for non-convex stochastic decentralized optimization with weight matrices defined over linear graphs, the optimal rate with general weight matrices remains unclear. This paper revisits non-convex stochastic decentralized optimization and establishes an optimal convergence rate with general weight matrices. In addition, we also establish the optimal rate when non-convex loss functions further satisfy the Polyak-Lojasiewicz (PL) condition. Following existing lines of analysis in literature cannot achieve these results. Instead, we leverage the Ring-Lattice graph to admit general weight matrices while maintaining the optimal relation between the graph diameter and weight matrix connectivity. Lastly, we develop a new decentralized algorithm to nearly attain the above two optimal rates under additional mild conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge