Rethinking SIGN Training: Provable Nonconvex Acceleration without First- and Second-Order Gradient Lipschitz
Paper and Code
Oct 23, 2023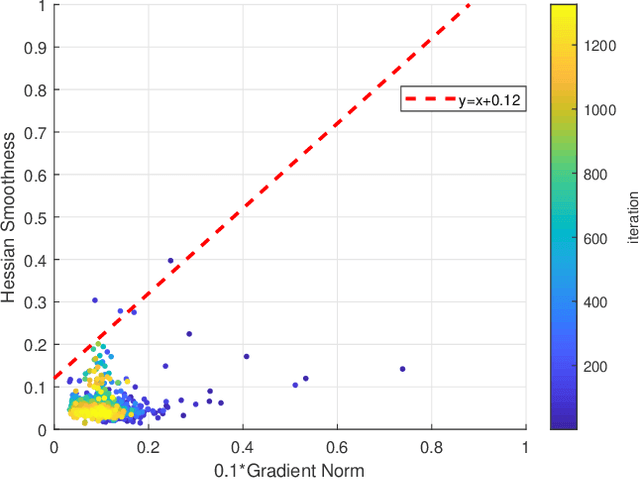
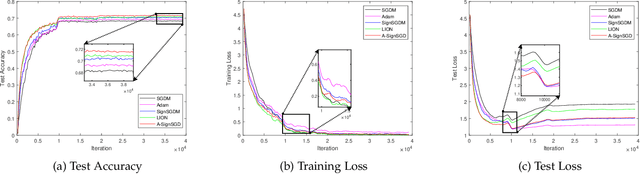
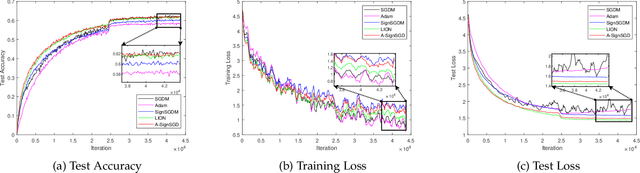
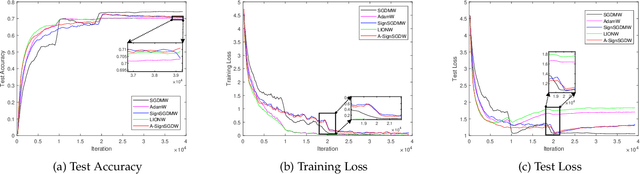
Sign-based stochastic methods have gained attention due to their ability to achieve robust performance despite using only the sign information for parameter updates. However, the current convergence analysis of sign-based methods relies on the strong assumptions of first-order gradient Lipschitz and second-order gradient Lipschitz, which may not hold in practical tasks like deep neural network training that involve high non-smoothness. In this paper, we revisit sign-based methods and analyze their convergence under more realistic assumptions of first- and second-order smoothness. We first establish the convergence of the sign-based method under weak first-order Lipschitz. Motivated by the weak first-order Lipschitz, we propose a relaxed second-order condition that still allows for nonconvex acceleration in sign-based methods. Based on our theoretical results, we gain insights into the computational advantages of the recently developed LION algorithm. In distributed settings, we prove that this nonconvex acceleration persists with linear speedup in the number of nodes, when utilizing fast communication compression gossip protocols. The novelty of our theoretical results lies in that they are derived under much weaker assumptions, thereby expanding the provable applicability of sign-based algorithms to a wider range of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge