Rethinking ResNets: Improved Stacking Strategies With High Order Schemes
Paper and Code
Apr 12, 2021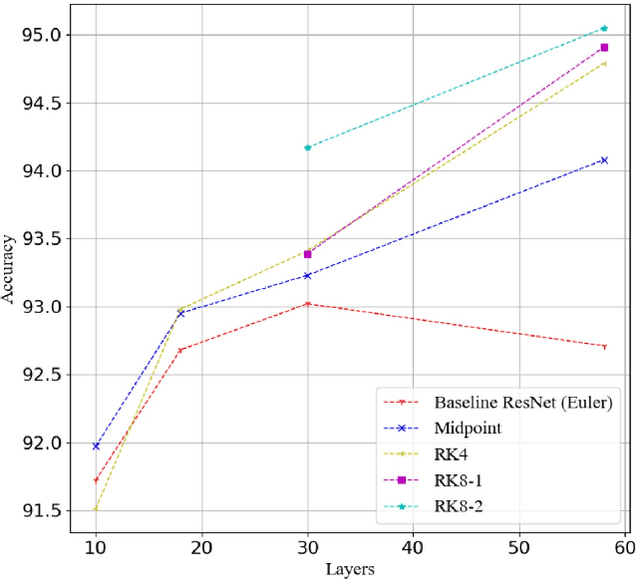

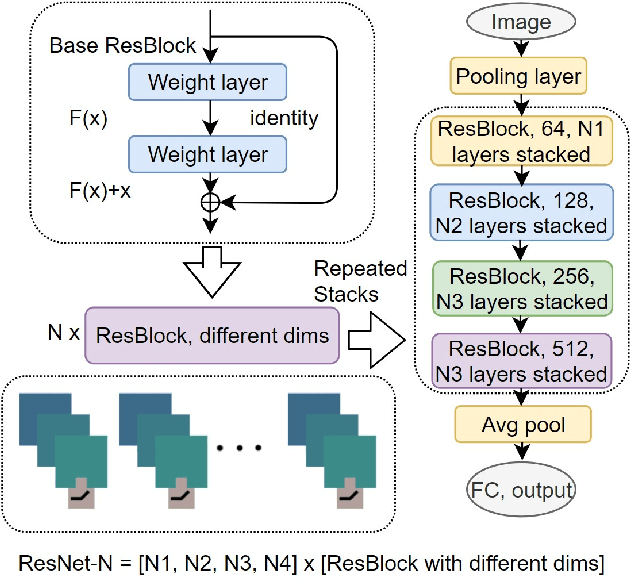
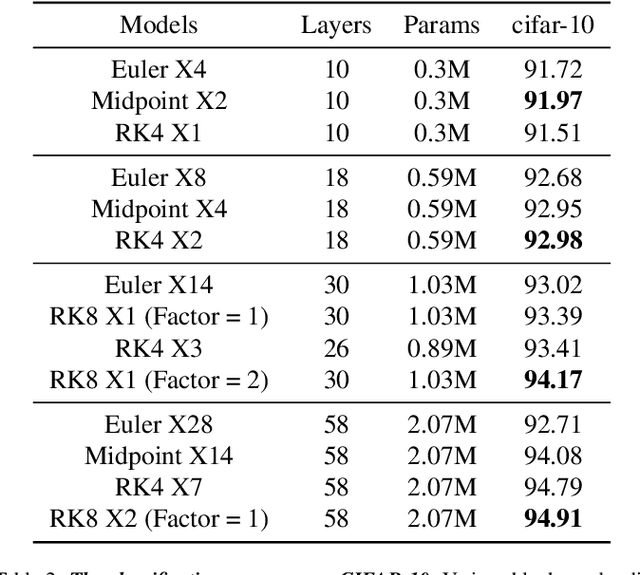
Various Deep Neural Network architectures are keeping massive vital records in computer vision. While drawing attention worldwide, the design of the overall structure somehow lacks general guidance. Based on the relationship between DNN design with numerical differential equations, which several researchers observed in recent years, we perform a fair comparison of residual design with higher-order perspectives. We show that the widely used DNN design strategy, constantly stacking a small design, could be easily improved, supported by solid theoretical knowledge and no extra parameters needed. We reorganize the residual design in higher-order ways, which is inspired by the observation that many effective networks could be interpreted as different numerical discretizations of differential equations. The design of ResNet follows a relatively simple scheme which is Euler forward; however, the situation is getting complicated rapidly while stacking. We suppose stacked ResNet is somehow equalled to a higher order scheme, then the current way of forwarding propagation might be relatively weak compared with a typical high-order method like Runge-Kutta. We propose higher order ResNet to verify the hypothesis on widely used CV benchmarks with sufficient experiments. Stable and noticeable rises in performance are observed, convergence and robustness are benefited.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge