Rethinking Persistent Homology for Visual Recognition
Paper and Code
Jul 09, 2022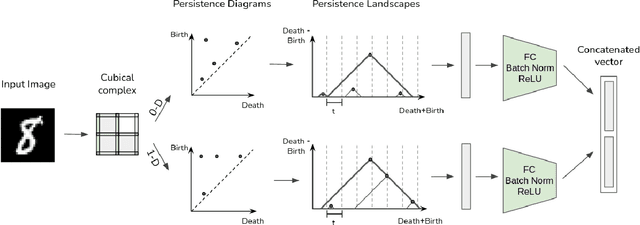
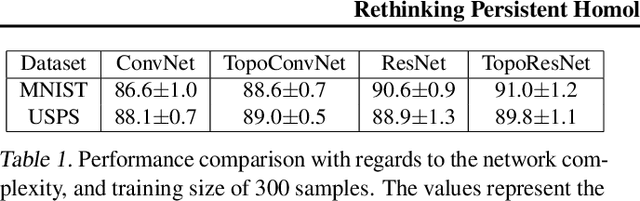
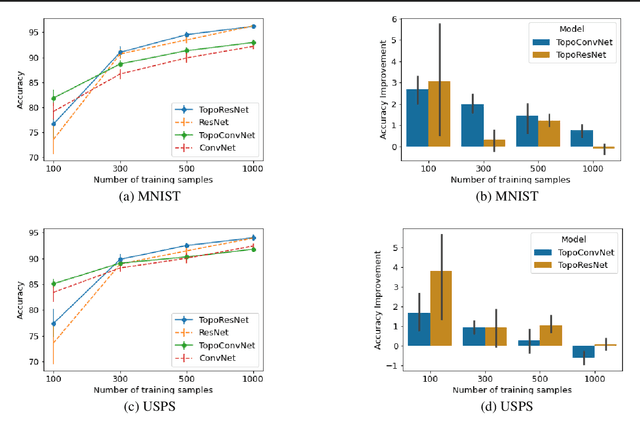
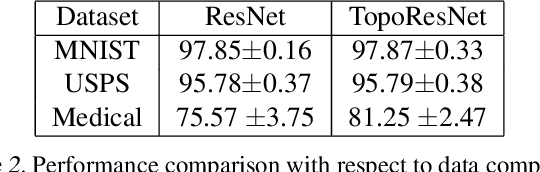
Persistent topological properties of an image serve as an additional descriptor providing an insight that might not be discovered by traditional neural networks. The existing research in this area focuses primarily on efficiently integrating topological properties of the data in the learning process in order to enhance the performance. However, there is no existing study to demonstrate all possible scenarios where introducing topological properties can boost or harm the performance. This paper performs a detailed analysis of the effectiveness of topological properties for image classification in various training scenarios, defined by: the number of training samples, the complexity of the training data and the complexity of the backbone network. We identify the scenarios that benefit the most from topological features, e.g., training simple networks on small datasets. Additionally, we discuss the problem of topological consistency of the datasets which is one of the major bottlenecks for using topological features for classification. We further demonstrate how the topological inconsistency can harm the performance for certain scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge