Resilient Consensus via Voronoi Communication Graphs
Paper and Code
Sep 20, 2022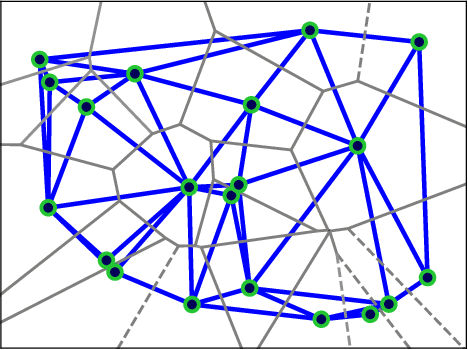
Consensus algorithms form the foundation for many distributed algorithms by enabling multiple robots to converge to consistent estimates of global variables using only local communication. However, standard consensus protocols can be easily led astray by non-cooperative team members. As such, the study of resilient forms of consensus is necessary for designing resilient distributed algorithms. W-MSR consensus is one such resilient consensus algorithm that allows for resilient consensus with only local knowledge of the communication graph and no a priori model for the data being shared. However, the verification that a given communication graph meets the strict graph connectivity requirement makes W-MSR difficult to use in practice. In this paper, we show that a commonly used communication graph structure in robotics literature, the communication graph built based on the Voronoi tessellation, automatically results in a sufficiently connected graph to reject a single non-cooperative team member. Further, we show how this graph can be enhanced to reject two non-cooperative team members and provide a roadmap for modifications for further resilience. This contribution will allow for the easy application of resilient consensus to algorithms that already rely on Voronoi-based communication such as distributed coverage and exploration algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge