Reinforcement Learning Control of Constrained Dynamic Systems with Uniformly Ultimate Boundedness Stability Guarantee
Paper and Code
Nov 13, 2020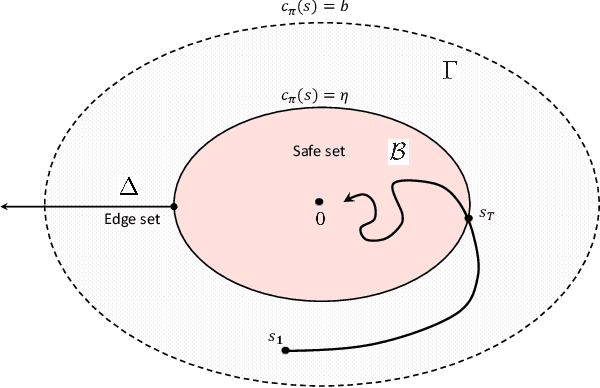



Reinforcement learning (RL) is promising for complicated stochastic nonlinear control problems. Without using a mathematical model, an optimal controller can be learned from data evaluated by certain performance criteria through trial-and-error. However, the data-based learning approach is notorious for not guaranteeing stability, which is the most fundamental property for any control system. In this paper, the classic Lyapunov's method is explored to analyze the uniformly ultimate boundedness stability (UUB) solely based on data without using a mathematical model. It is further shown how RL with UUB guarantee can be applied to control dynamic systems with safety constraints. Based on the theoretical results, both off-policy and on-policy learning algorithms are proposed respectively. As a result, optimal controllers can be learned to guarantee UUB of the closed-loop system both at convergence and during learning. The proposed algorithms are evaluated on a series of robotic continuous control tasks with safety constraints. In comparison with the existing RL algorithms, the proposed method can achieve superior performance in terms of maintaining safety. As a qualitative evaluation of stability, our method shows impressive resilience even in the presence of external disturbances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge