Quasi-Newton OMP Approach for Super-Resolution Channel Estimation and Extrapolation
Paper and Code
Nov 09, 2024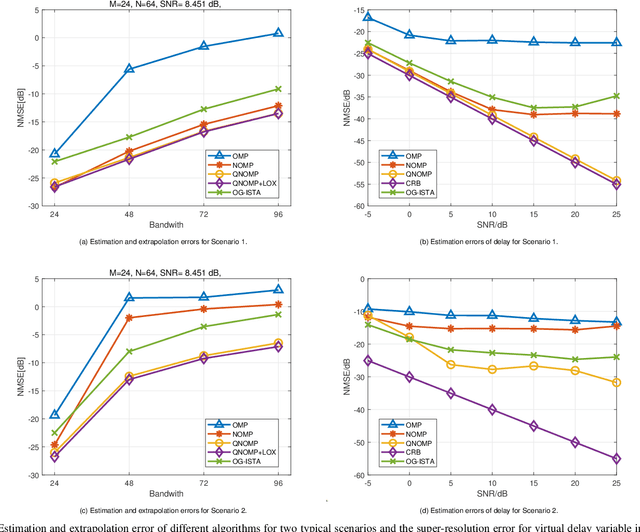
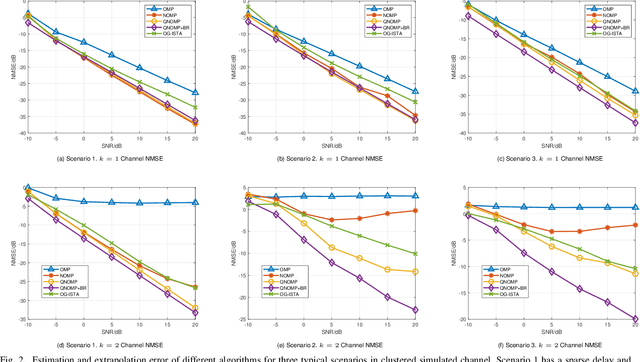
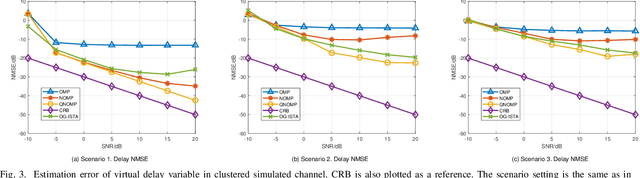
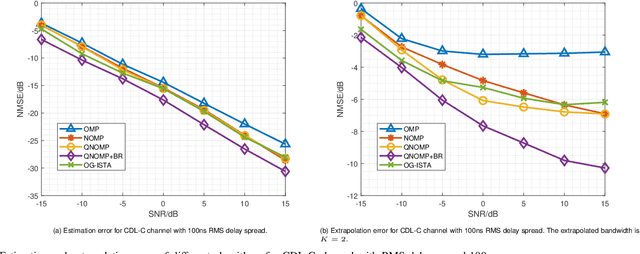
Channel estimation and extrapolation are fundamental issues in MIMO communication systems. In this paper, we proposed the quasi-Newton orthogonal matching pursuit (QNOMP) approach to overcome these issues with high efficiency while maintaining accuracy. The algorithm consists of two stages on the super-resolution recovery: we first performed a cheap on-grid OMP estimation of channel parameters in the sparsity domain (e.g., delay or angle), then an off-grid optimization to achieve the super-resolution. In the off-grid stage, we employed the BFGS quasi-Newton method to jointly estimate the parameters through a multipath model, which improved the speed and accuracy significantly. Furthermore, we derived the optimal extrapolated solution in the linear minimum mean squared estimator criterion, revealed its connection with Slepian basis, and presented a practical algorithm to realize the extrapolation based on the QNOMP results. Special treatment utilizing the block sparsity nature of the considered channels was also proposed. Numerical experiments on the simulated models and CDL-C channels demonstrated the high performance and low computational complexity of QNOMP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge