Quasi-Conservative Score-based Generative Models
Paper and Code
Sep 26, 2022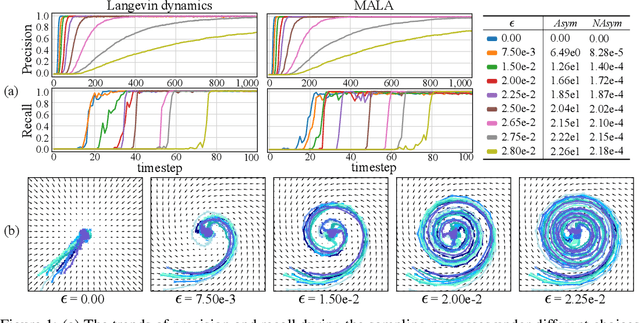
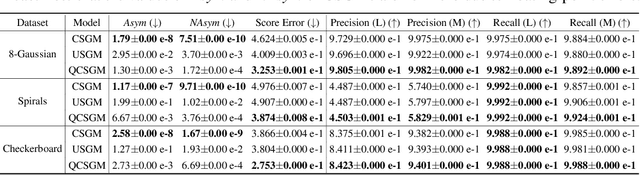
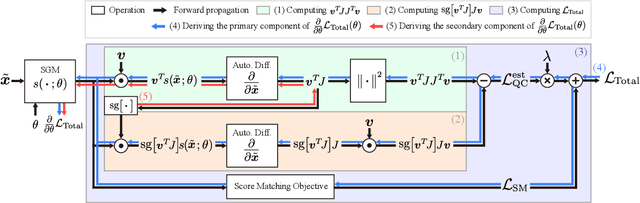
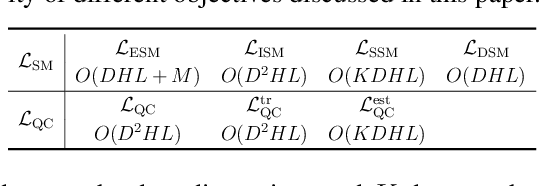
Existing Score-based Generative Models (SGMs) can be categorized into constrained SGMs (CSGMs) or unconstrained SGMs (USGMs) according to their parameterization approaches. CSGMs model the probability density functions as Boltzmann distributions, and assign their predictions as the negative gradients of some scalar-valued energy functions. On the other hand, USGMs employ flexible architectures capable of directly estimating scores without the need to explicitly model energy functions. In this paper, we demonstrate that the architectural constraints of CSGMs may limit their score-matching ability. In addition, we show that USGMs' inability to preserve the property of conservativeness may lead to serious sampling inefficiency and degraded sampling performance in practice. To address the above issues, we propose Quasi-Conservative Score-based Generative Models (QCSGMs) for keeping the advantages of both CSGMs and USGMs. Our theoretical derivations demonstrate that the training objective of QCSGMs can be efficiently integrated into the training processes by leveraging the Hutchinson trace estimator. In addition, our experimental results on the Cifar-10, Cifar-100, ImageNet, and SVHN datasets validate the effectiveness of QCSGMs. Finally, we justify the advantage of QCSGMs using an example of a one-layered autoencoder.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge