Quantum Clustering with k-Means: a Hybrid Approach
Paper and Code
Dec 15, 2022
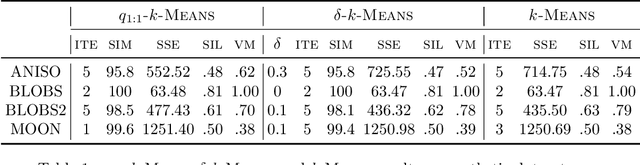
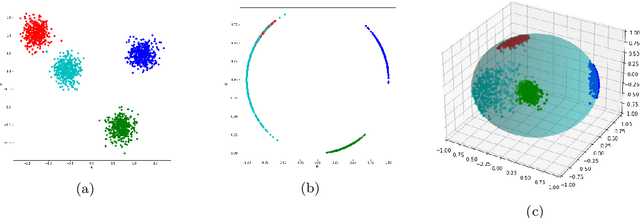
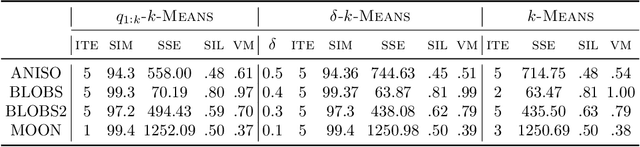
Quantum computing is a promising paradigm based on quantum theory for performing fast computations. Quantum algorithms are expected to surpass their classical counterparts in terms of computational complexity for certain tasks, including machine learning. In this paper, we design, implement, and evaluate three hybrid quantum k-Means algorithms, exploiting different degree of parallelism. Indeed, each algorithm incrementally leverages quantum parallelism to reduce the complexity of the cluster assignment step up to a constant cost. In particular, we exploit quantum phenomena to speed up the computation of distances. The core idea is that the computation of distances between records and centroids can be executed simultaneously, thus saving time, especially for big datasets. We show that our hybrid quantum k-Means algorithms can be more efficient than the classical version, still obtaining comparable clustering results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge