Proving $μ>1$
Paper and Code
May 13, 2020

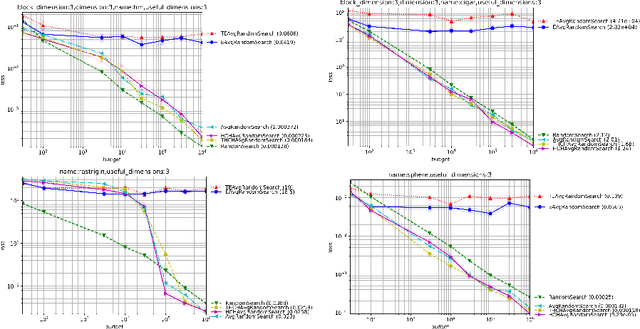
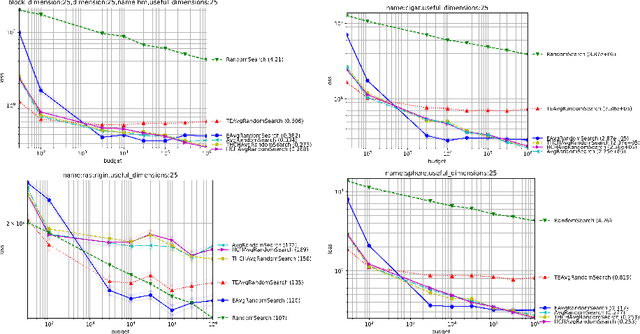
Choosing the right selection rate is a long standing issue in evolutionary computation. In the continuous unconstrained case, we prove mathematically that $\mu=1$ leads to a sub-optimal simple regret in the case of the sphere function. We provide a theoretically-based selection rate $\mu/\lambda$ that leads to better convergence rates. With our choice of selection rate, we get a provable regret of order $O(\lambda^{-1})$ which has to be compared with $O(\lambda^{-2/d})$ in the case where $\mu=1$. We complete our study with experiments to confirm our theoretical claims.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge