Provably Accelerated Decentralized Gradient Method Over Unbalanced Directed Graphs
Paper and Code
Jul 26, 2021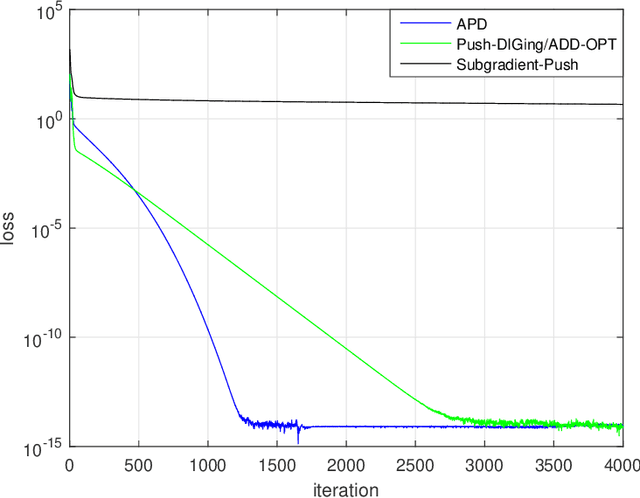
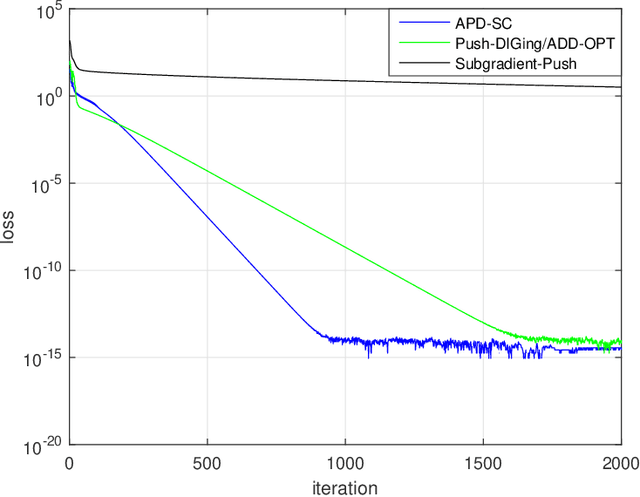
In this work, we consider the decentralized optimization problem in which a network of $n$ agents, each possessing a smooth and convex objective function, wish to collaboratively minimize the average of all the objective functions through peer-to-peer communication in a directed graph. To solve the problem, we propose two accelerated Push-DIGing methods termed APD and APD-SC for minimizing non-strongly convex objective functions and strongly convex ones, respectively. We show that APD and APD-SC respectively converge at the rates $O\left(\frac{1}{k^2}\right)$ and $O\left(\left(1 - C\sqrt{\frac{\mu}{L}}\right)^k\right)$ up to constant factors depending only on the mixing matrix. To the best of our knowledge, APD and APD-SC are the first decentralized methods to achieve provable acceleration over unbalanced directed graphs. Numerical experiments demonstrate the effectiveness of both methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge