Provable Memorization via Deep Neural Networks using Sub-linear Parameters

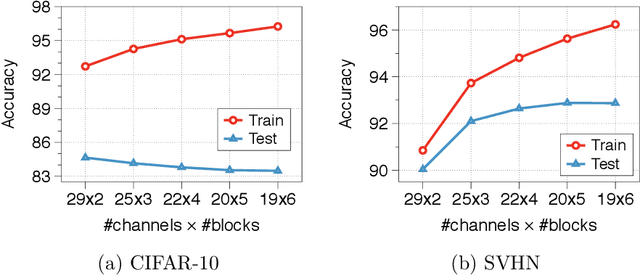
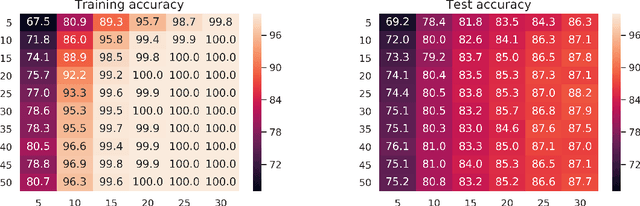
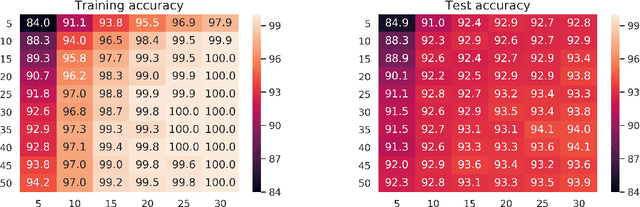
It is known that $\Theta(N)$ parameters are sufficient for neural networks to memorize arbitrary $N$ input-label pairs. By exploiting depth, we show that $\Theta(N^{2/3})$ parameters suffice to memorize $N$ pairs, under a mild condition on the separation of input points. In particular, deeper networks (even with width $3$) are shown to memorize more pairs than shallow networks, which also agrees with the recent line of works on the benefits of depth for function approximation. We also provide empirical results that support our theoretical findings.