Propagating Uncertainty through the tanh Function with Application to Reservoir Computing

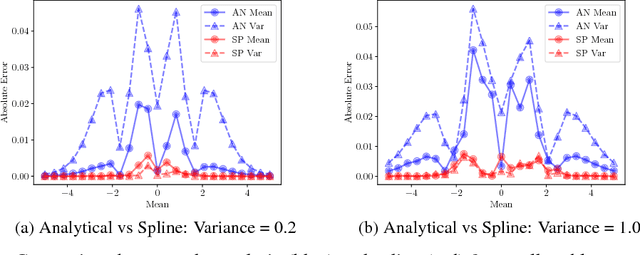
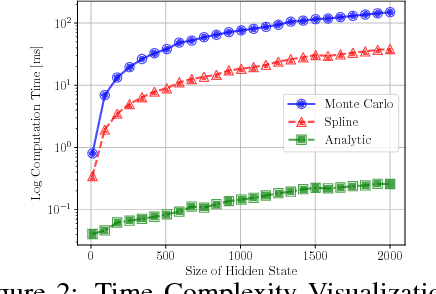
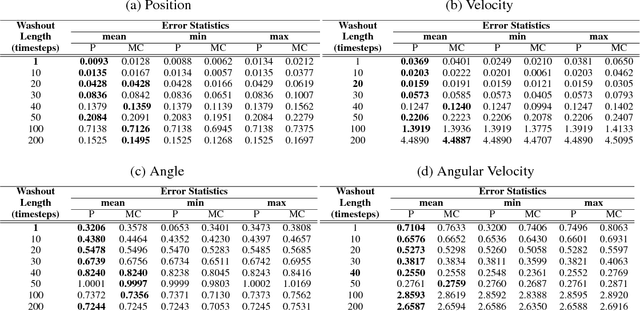
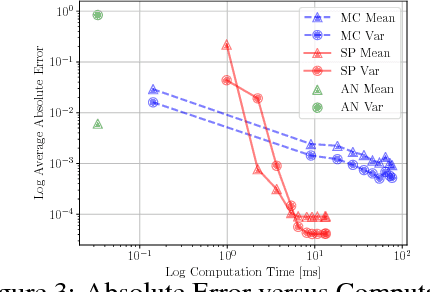
Many neural networks use the tanh activation function, however when given a probability distribution as input, the problem of computing the output distribution in neural networks with tanh activation has not yet been addressed. One important example is the initialization of the echo state network in reservoir computing, where random initialization of the reservoir requires time to wash out the initial conditions, thereby wasting precious data and computational resources. Motivated by this problem, we propose a novel solution utilizing a moment based approach to propagate uncertainty through an Echo State Network to reduce the washout time. In this work, we contribute two new methods to propagate uncertainty through the tanh activation function and propose the Probabilistic Echo State Network (PESN), a method that is shown to have better average performance than deterministic Echo State Networks given the random initialization of reservoir states. Additionally we test single and multi-step uncertainty propagation of our method on two regression tasks and show that we are able to recover similar means and variances as computed by Monte-Carlo simulations.