Progressive Batching for Efficient Non-linear Least Squares
Paper and Code
Oct 21, 2020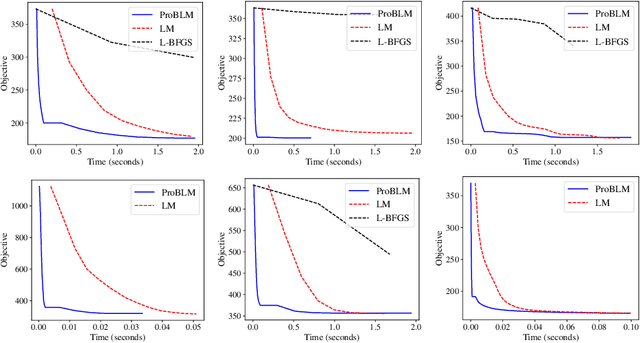
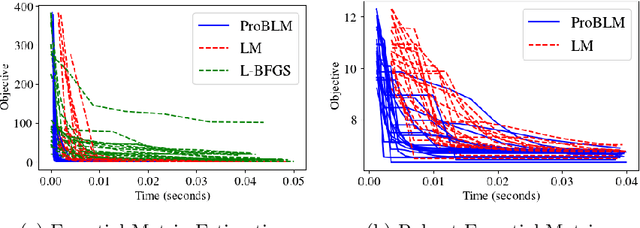
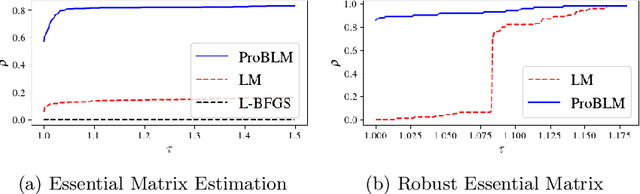
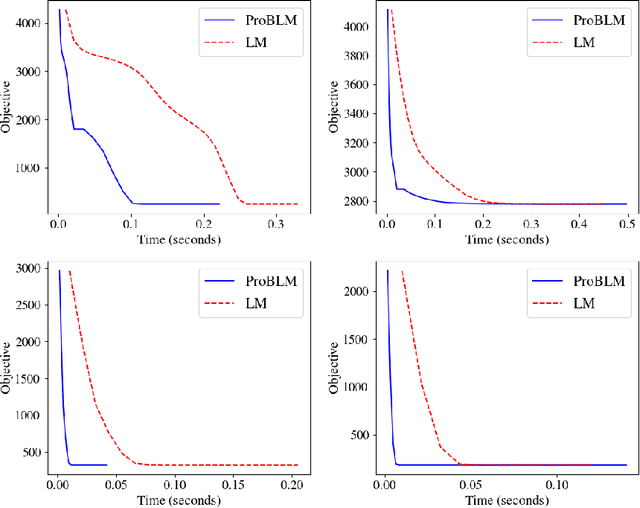
Non-linear least squares solvers are used across a broad range of offline and real-time model fitting problems. Most improvements of the basic Gauss-Newton algorithm tackle convergence guarantees or leverage the sparsity of the underlying problem structure for computational speedup. With the success of deep learning methods leveraging large datasets, stochastic optimization methods received recently a lot of attention. Our work borrows ideas from both stochastic machine learning and statistics, and we present an approach for non-linear least-squares that guarantees convergence while at the same time significantly reduces the required amount of computation. Empirical results show that our proposed method achieves competitive convergence rates compared to traditional second-order approaches on common computer vision problems, such as image alignment and essential matrix estimation, with very large numbers of residuals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge