Probabilistic Spatial Transformers for Bayesian Data Augmentation
Paper and Code
Apr 07, 2020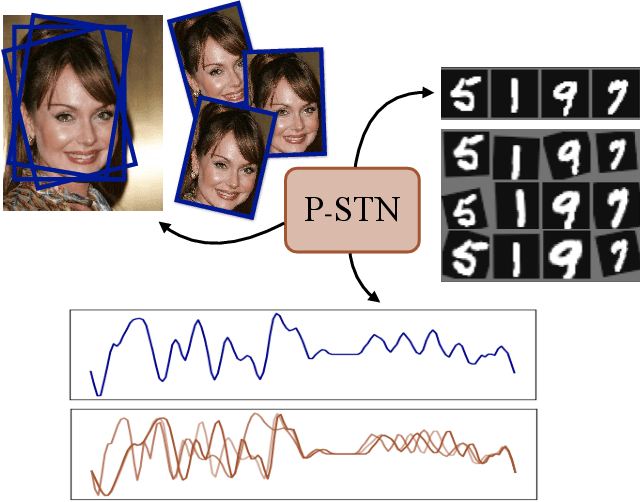
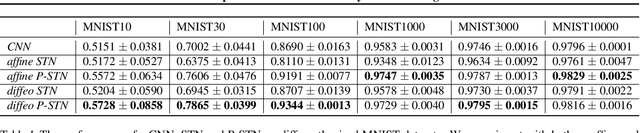
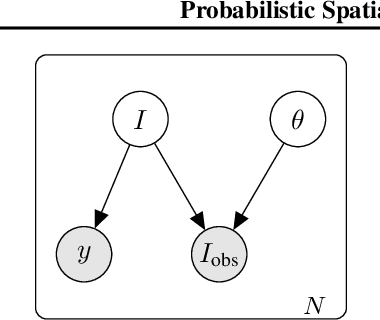

High-capacity models require vast amounts of data, and data augmentation is a common remedy when this resource is limited. Standard augmentation techniques apply small hand-tuned transformations to existing data, which is a brittle process that realistically only allows for simple transformations. We propose a Bayesian interpretation of data augmentation where the transformations are modelled as latent variables to be marginalized, and show how these can be inferred variationally in an end-to-end fashion. This allows for significantly more complex transformations than manual tuning, and the marginalization implies a form of test-time data augmentation. The resulting model can be interpreted as a probabilistic extension of spatial transformer networks. Experimentally, we demonstrate improvements in accuracy and uncertainty quantification in image and time series classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge