Probabilistic Conformal Prediction Using Conditional Random Samples
Paper and Code
Jun 20, 2022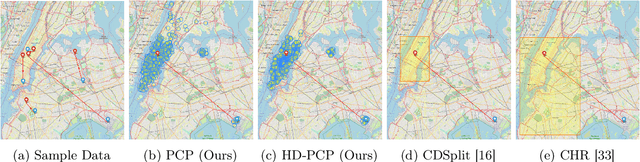
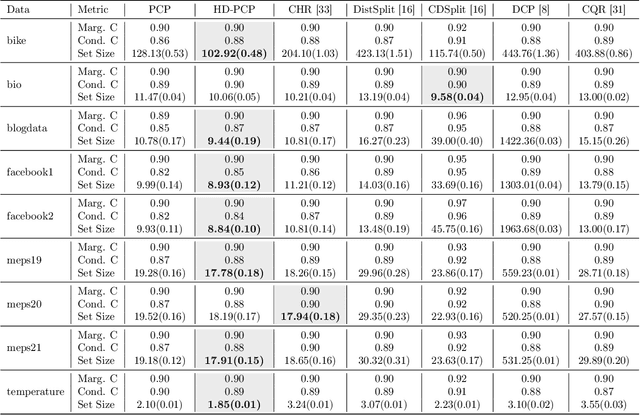
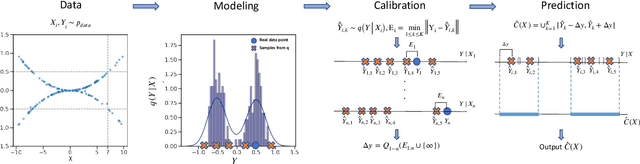

This paper proposes probabilistic conformal prediction (PCP), a predictive inference algorithm that estimates a target variable by a discontinuous predictive set. Given inputs, PCP construct the predictive set based on random samples from an estimated generative model. It is efficient and compatible with either explicit or implicit conditional generative models. Theoretically, we show that PCP guarantees correct marginal coverage with finite samples. Empirically, we study PCP on a variety of simulated and real datasets. Compared to existing methods for conformal inference, PCP provides sharper predictive sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge