Privacy-preserving Transfer Learning for Knowledge Sharing
Paper and Code
Nov 23, 2018
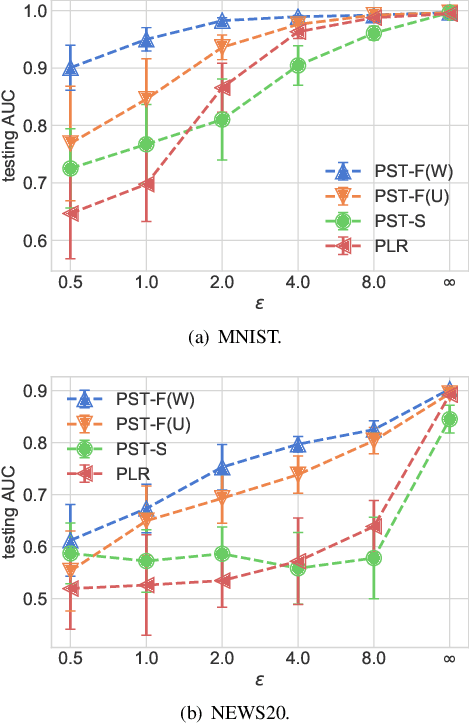
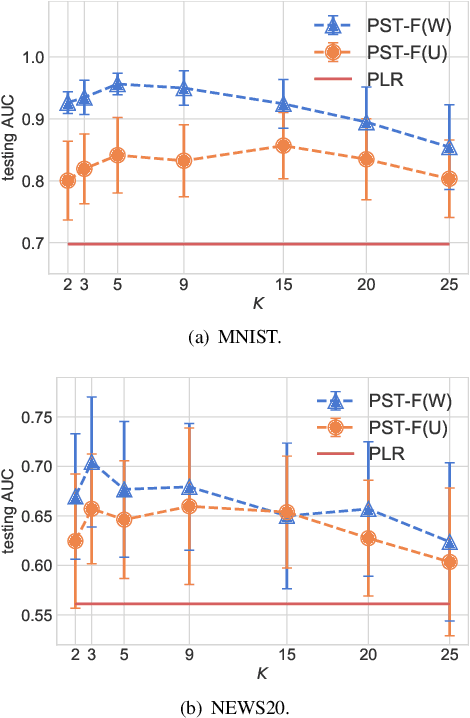

In many practical machine-learning applications, it is critical to allow knowledge to be transferred from external domains while preserving user privacy. Unfortunately, existing transfer-learning works do not have a privacy guarantee. In this paper, for the first time, we propose a method that can simultaneously transfer knowledge from external datasets while offering an $\epsilon$-differential privacy guarantee. First, we show that a simple combination of the hypothesis transfer learning and the privacy preserving logistic regression can address the problem. However, the performance of this approach can be poor as the sample size in the target domain may be small. To address this problem, we propose a new method which splits the feature set in source and target data into several subsets, and trains models on these subsets before finally aggregating the predictions by a stacked generalization. Feature importance can also be incorporated into the proposed method to further improve performance. We prove that the proposed method has an $\epsilon$-differential privacy guarantee, and further analysis shows that its performance is better than above simple combination given the same privacy budget. Finally, experiments on MINST and real-world RUIJIN datasets show that our proposed method achieves the start-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge