Prediction Error Meta Classification in Semantic Segmentation: Detection via Aggregated Dispersion Measures of Softmax Probabilities
Paper and Code
Nov 01, 2018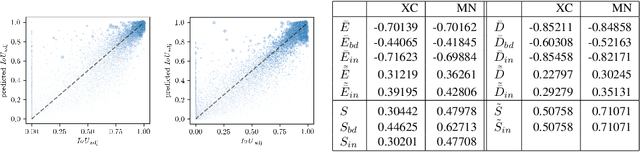
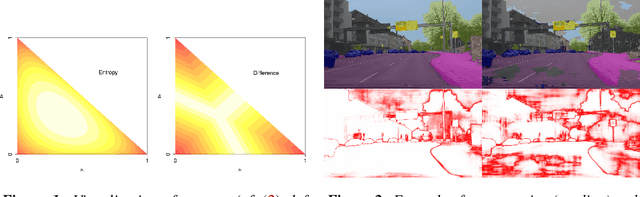
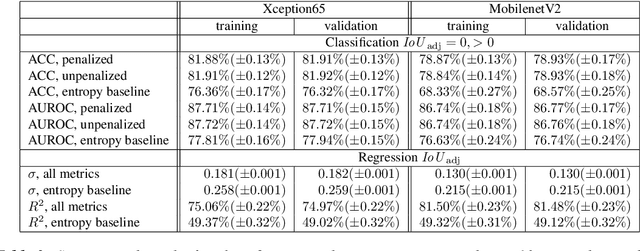
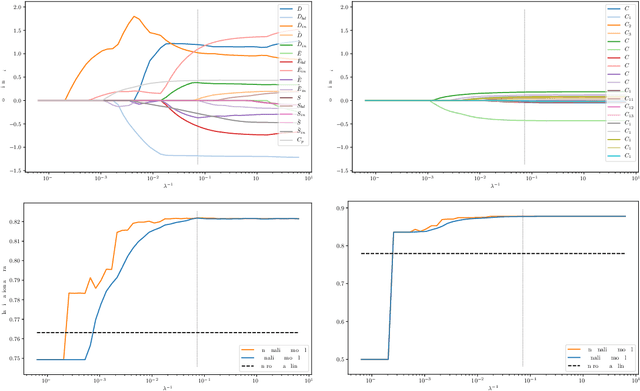
We present a method that "meta" classifies whether segments (objects) predicted by a semantic segmentation neural network intersect with the ground truth. To this end, we employ measures of dispersion for predicted pixel-wise class probability distributions, like classification entropy, that yield heat maps of the input scene's size. We aggregate these dispersion measures segment-wise and derive metrics that are well-correlated with the segment-wise $\mathit{IoU}$ of prediction and ground truth. In our tests, we use two publicly available DeepLabv3+ networks (pre-trained on the Cityscapes data set) and analyze the predictive power of different metrics and different sets of metrics. To this end, we compute logistic LASSO regression fits for the task of classifying $\mathit{IoU}=0$ vs. $\mathit{IoU} > 0$ per segment and obtain classification rates of up to $81.91\%$ and AUROC values of up to $87.71\%$ without the incorporation of advanced techniques like Monte-Carlo dropout. We complement these tests with linear regression fits to predict the segment-wise $\mathit{IoU}$ and obtain prediction standard deviations of down to $0.130$ as well as $R^2$ values of up to $81.48\%$. We show that these results clearly outperform single-metric baseline approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge