Practical Fixed-Parameter Algorithms for Defending Active Directory Style Attack Graphs
Paper and Code
Dec 25, 2021

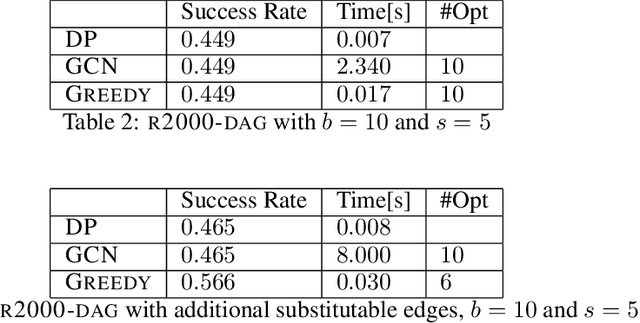
Active Directory is the default security management system for Windows domain networks. We study the shortest path edge interdiction problem for defending Active Directory style attack graphs. The problem is formulated as a Stackelberg game between one defender and one attacker. The attack graph contains one destination node and multiple entry nodes. The attacker's entry node is chosen by nature. The defender chooses to block a set of edges limited by his budget. The attacker then picks the shortest unblocked attack path. The defender aims to maximize the expected shortest path length for the attacker, where the expectation is taken over entry nodes. We observe that practical Active Directory attack graphs have small maximum attack path lengths and are structurally close to trees. We first show that even if the maximum attack path length is a constant, the problem is still $W[1]$-hard with respect to the defender's budget. Having a small maximum attack path length and a small budget is not enough to design fixed-parameter algorithms. If we further assume that the number of entry nodes is small, then we derive a fixed-parameter tractable algorithm. We then propose two other fixed-parameter algorithms by exploiting the tree-like features. One is based on tree decomposition and requires a small tree width. The other assumes a small number of splitting nodes (nodes with multiple out-going edges). Finally, the last algorithm is converted into a graph convolutional neural network based heuristic, which scales to larger graphs with more splitting nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge