Planning with Learned Dynamics: Guaranteed Safety and Reachability via Lipschitz Constants
Paper and Code
Oct 18, 2020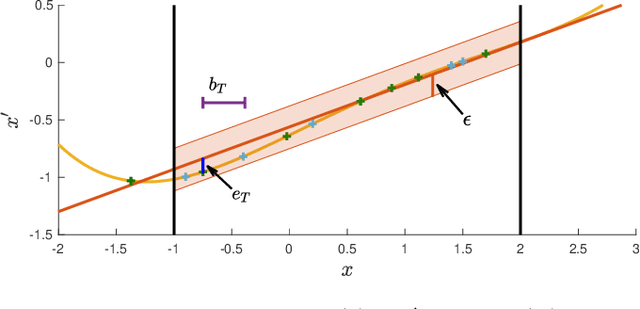
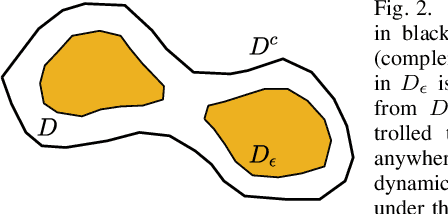
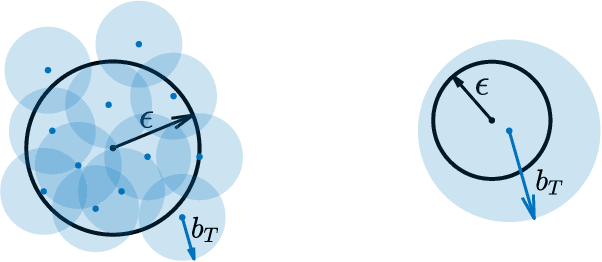
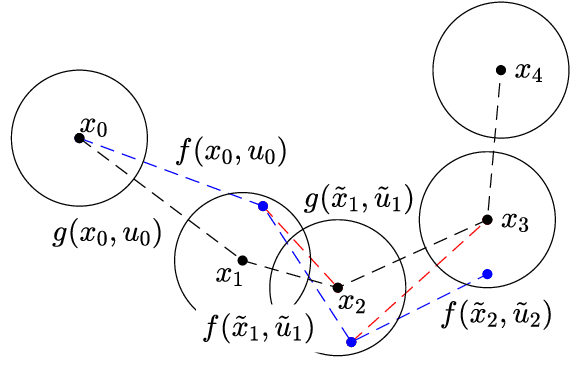
We present an approach for feedback motion planning of systems with unknown dynamics which provides guarantees on safety, reachability, and stability about the goal. Given a learned control-affine approximation of the true dynamics, we estimate the Lipschitz constant of the difference between the true and learned dynamics to determine a trusted domain for our learned model. Provided the system has at least as many controls as states, we further derive the conditions under which a one-step feedback law exists. This allows fora small bound on the tracking error when the trajectory is executed on the real system. Our method imposes a check for the existence of the feedback law as constraints in a sampling-based planner, which returns a feedback policy ensuring that under the true dynamics, the goal is reachable, the path is safe in execution, and the closed-loop system is invariant in a small set about the goal. We demonstrate our approach by planning using learned models of a 6D quadrotor and a 7DOF Kuka arm.We show that a baseline which plans using the same learned dynamics without considering the error bound or the existence of the feedback law can fail to stabilize around the plan and become unsafe.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge