PL-kNN: A Parameterless Nearest Neighbors Classifier
Paper and Code
Sep 30, 2022

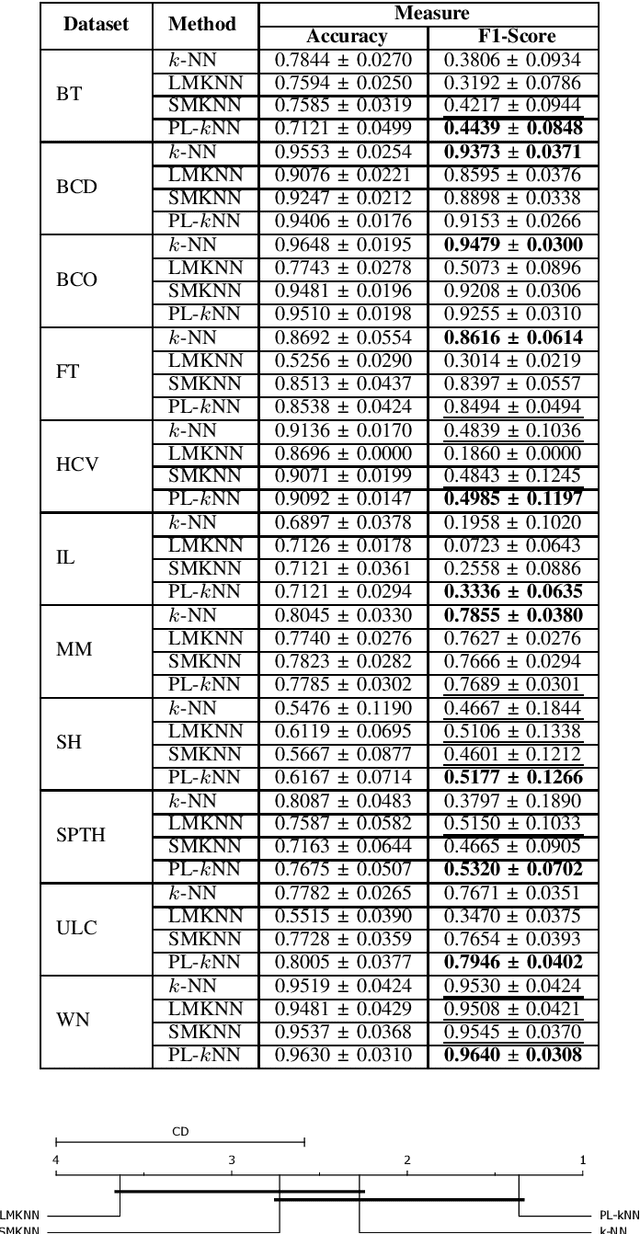
Demands for minimum parameter setup in machine learning models are desirable to avoid time-consuming optimization processes. The $k$-Nearest Neighbors is one of the most effective and straightforward models employed in numerous problems. Despite its well-known performance, it requires the value of $k$ for specific data distribution, thus demanding expensive computational efforts. This paper proposes a $k$-Nearest Neighbors classifier that bypasses the need to define the value of $k$. The model computes the $k$ value adaptively considering the data distribution of the training set. We compared the proposed model against the standard $k$-Nearest Neighbors classifier and two parameterless versions from the literature. Experiments over 11 public datasets confirm the robustness of the proposed approach, for the obtained results were similar or even better than its counterpart versions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge