PIE-NeRF: Physics-based Interactive Elastodynamics with NeRF
Paper and Code
Nov 22, 2023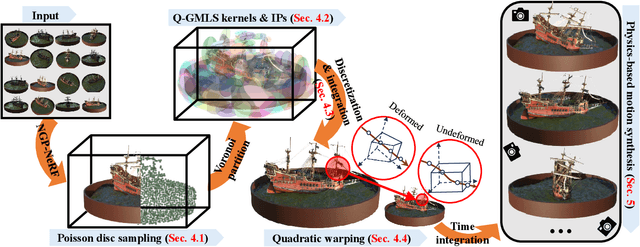
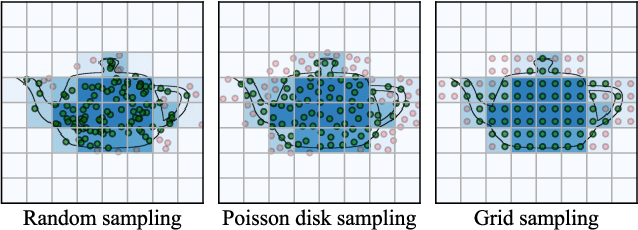


We show that physics-based simulations can be seamlessly integrated with NeRF to generate high-quality elastodynamics of real-world objects. Unlike existing methods, we discretize nonlinear hyperelasticity in a meshless way, obviating the necessity for intermediate auxiliary shape proxies like a tetrahedral mesh or voxel grid. A quadratic generalized moving least square (Q-GMLS) is employed to capture nonlinear dynamics and large deformation on the implicit model. Such meshless integration enables versatile simulations of complex and codimensional shapes. We adaptively place the least-square kernels according to the NeRF density field to significantly reduce the complexity of the nonlinear simulation. As a result, physically realistic animations can be conveniently synthesized using our method for a wide range of hyperelastic materials at an interactive rate. For more information, please visit our project page at https://fytalon.github.io/pienerf/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge