Performance Analysis of Physical Layer Security: From Far-Field to Near-Field
Paper and Code
Aug 20, 2024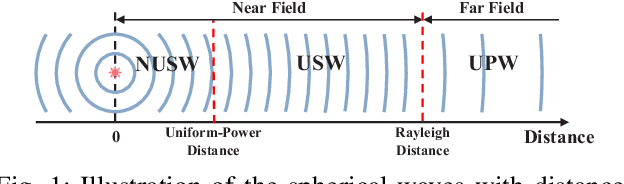
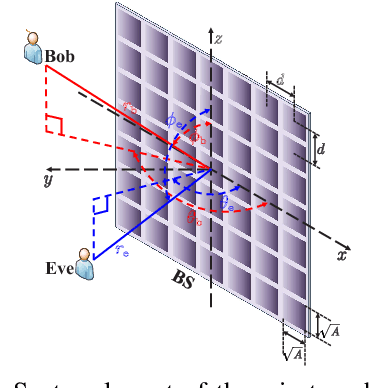
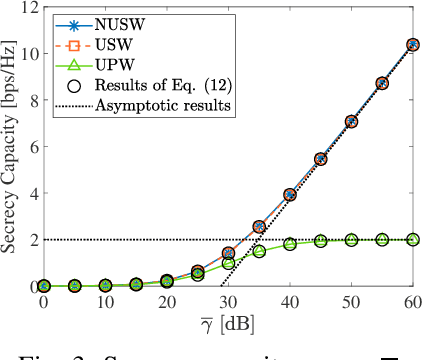
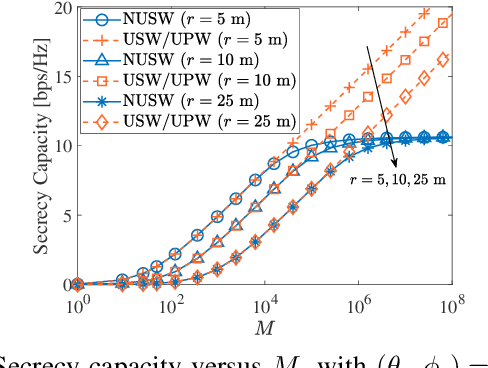
The secrecy performance in both near-field and far-field communications is analyzed using two fundamental metrics: the secrecy capacity under a power constraint and the minimum power requirement to achieve a specified secrecy rate target. 1) For the secrecy capacity, a closed-form expression is derived under a discrete-time memoryless setup. This expression is further analyzed under several far-field and near-field channel models, and the capacity scaling law is revealed by assuming an infinitely large transmit array and an infinitely high power. A novel concept of "depth of insecurity" is proposed to evaluate the secrecy performance achieved by near-field beamfocusing. It is demonstrated that increasing the number of transmit antennas reduces this depth and thus improves the secrecy performance. 2) Regarding the minimum required power, a closed-form expression is derived and analyzed within far-field and near-field scenarios. Asymptotic analyses are performed by setting the number of transmit antennas to infinity to unveil the power scaling law. Numerical results are provided to demonstrate that: i) compared to far-field communications, near-field communications expand the areas where secure transmission is feasible, specifically when the eavesdropper is located in the same direction as the intended receiver; ii) as the number of transmit antennas increases, neither the secrecy capacity nor the minimum required power scales or vanishes unboundedly, adhering to the principle of energy conservation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge