PDO-s3DCNNs: Partial Differential Operator Based Steerable 3D CNNs
Paper and Code
Aug 07, 2022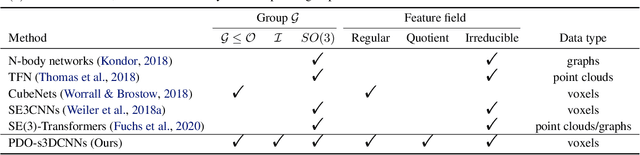
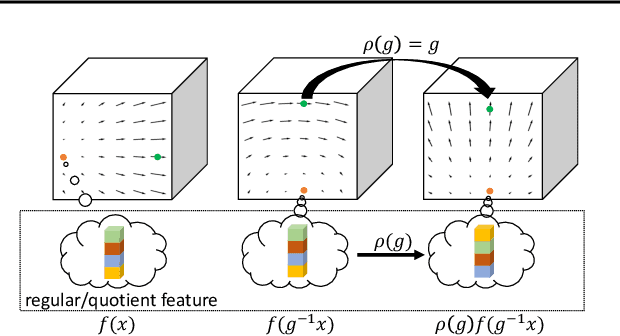

Steerable models can provide very general and flexible equivariance by formulating equivariance requirements in the language of representation theory and feature fields, which has been recognized to be effective for many vision tasks. However, deriving steerable models for 3D rotations is much more difficult than that in the 2D case, due to more complicated mathematics of 3D rotations. In this work, we employ partial differential operators (PDOs) to model 3D filters, and derive general steerable 3D CNNs, which are called PDO-s3DCNNs. We prove that the equivariant filters are subject to linear constraints, which can be solved efficiently under various conditions. As far as we know, PDO-s3DCNNs are the most general steerable CNNs for 3D rotations, in the sense that they cover all common subgroups of $SO(3)$ and their representations, while existing methods can only be applied to specific groups and representations. Extensive experiments show that our models can preserve equivariance well in the discrete domain, and outperform previous works on SHREC'17 retrieval and ISBI 2012 segmentation tasks with a low network complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge