PDO-e$\text{S}^\text{2}$CNNs: Partial Differential Operator Based Equivariant Spherical CNNs

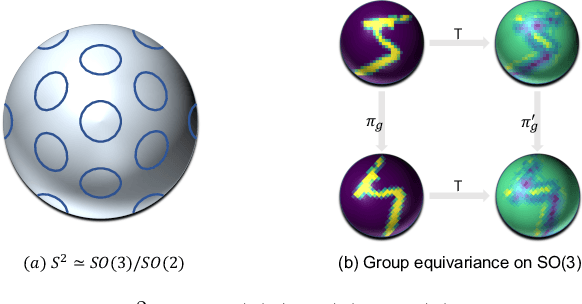
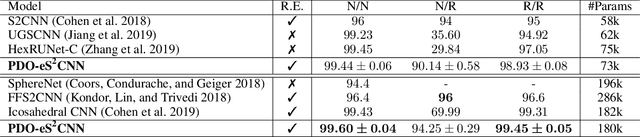
Spherical signals exist in many applications, e.g., planetary data, LiDAR scans and digitalization of 3D objects, calling for models that can process spherical data effectively. It does not perform well when simply projecting spherical data into the 2D plane and then using planar convolution neural networks (CNNs), because of the distortion from projection and ineffective translation equivariance. Actually, good principles of designing spherical CNNs are avoiding distortions and converting the shift equivariance property in planar CNNs to rotation equivariance in the spherical domain. In this work, we use partial differential operators (PDOs) to design a spherical equivariant CNN, PDO-e$\text{S}^\text{2}$CNN, which is exactly rotation equivariant in the continuous domain. We then discretize PDO-e$\text{S}^\text{2}$CNNs, and analyze the equivariance error resulted from discretization. This is the first time that the equivariance error is theoretically analyzed in the spherical domain. In experiments, PDO-e$\text{S}^\text{2}$CNNs show greater parameter efficiency and outperform other spherical CNNs significantly on several tasks.