Particle-Filtering-based Latent Diffusion for Inverse Problems
Paper and Code
Aug 25, 2024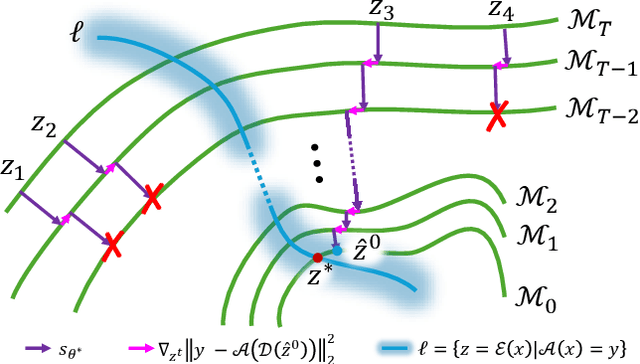
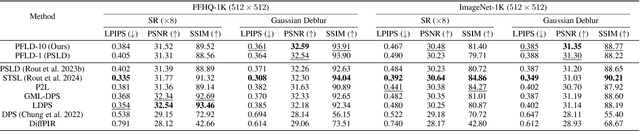
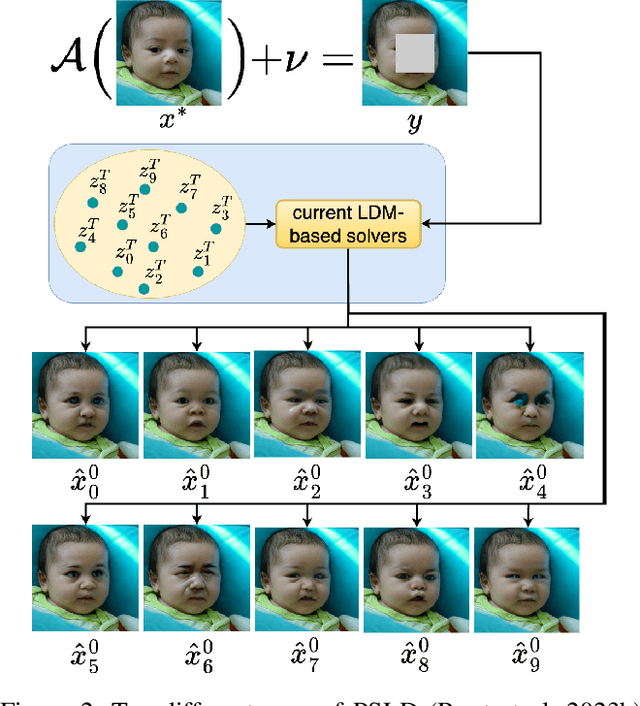

Current strategies for solving image-based inverse problems apply latent diffusion models to perform posterior sampling.However, almost all approaches make no explicit attempt to explore the solution space, instead drawing only a single sample from a Gaussian distribution from which to generate their solution. In this paper, we introduce a particle-filtering-based framework for a nonlinear exploration of the solution space in the initial stages of reverse SDE methods. Our proposed particle-filtering-based latent diffusion (PFLD) method and proposed problem formulation and framework can be applied to any diffusion-based solution for linear or nonlinear inverse problems. Our experimental results show that PFLD outperforms the SoTA solver PSLD on the FFHQ-1K and ImageNet-1K datasets on inverse problem tasks of super resolution, Gaussian debluring and inpainting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge