Partial Gromov-Wasserstein Learning for Partial Graph Matching
Paper and Code
Dec 09, 2020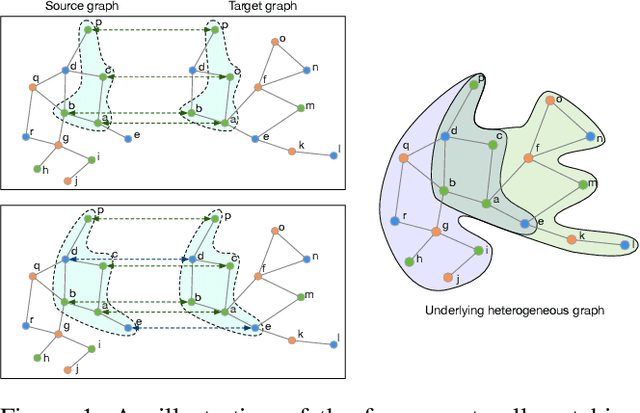
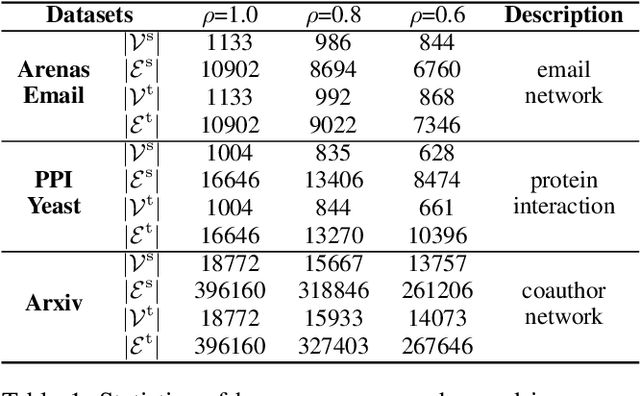
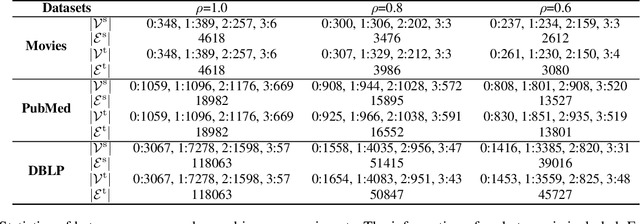
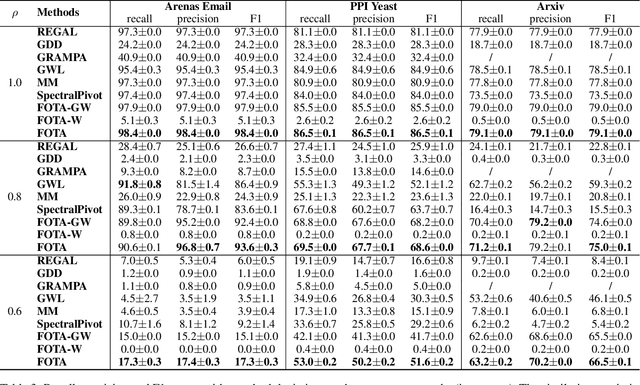
Graph matching finds the correspondence of nodes across two graphs and is a basic task in graph-based machine learning. Numerous existing methods match every node in one graph to one node in the other graph whereas two graphs usually overlap partially in many \realworld{} applications. In this paper, a partial Gromov-Wasserstein learning framework is proposed for partially matching two graphs, which fuses the partial Gromov-Wasserstein distance and the partial Wasserstein distance as the objective and updates the partial transport map and the node embedding in an alternating fashion. The proposed framework transports a fraction of the probability mass and matches node pairs with high relative similarities across the two graphs. Incorporating an embedding learning method, heterogeneous graphs can also be matched. Numerical experiments on both synthetic and \realworld{} graphs demonstrate that our framework can improve the F1 score by at least $20\%$ and often much more.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge