Parametric Return Density Estimation for Reinforcement Learning
Paper and Code
Mar 15, 2012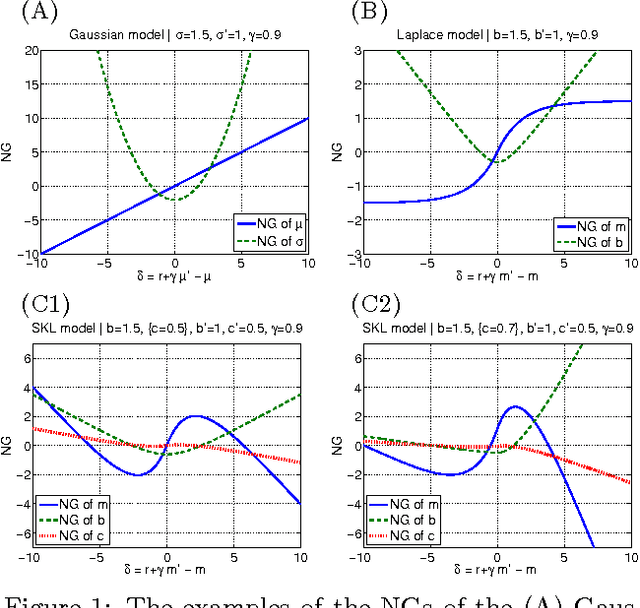
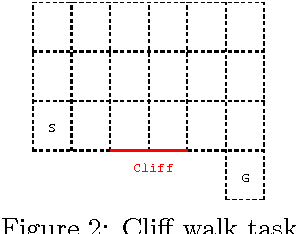
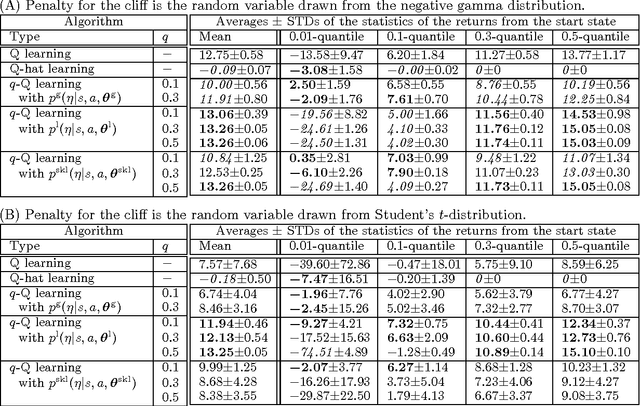
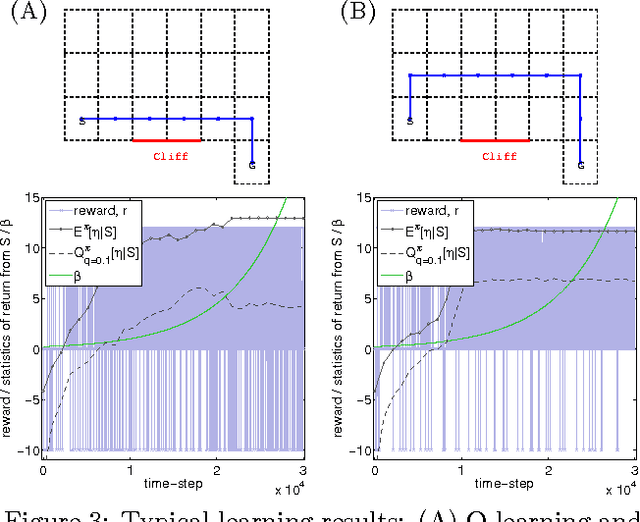
Most conventional Reinforcement Learning (RL) algorithms aim to optimize decision-making rules in terms of the expected returns. However, especially for risk management purposes, other risk-sensitive criteria such as the value-at-risk or the expected shortfall are sometimes preferred in real applications. Here, we describe a parametric method for estimating density of the returns, which allows us to handle various criteria in a unified manner. We first extend the Bellman equation for the conditional expected return to cover a conditional probability density of the returns. Then we derive an extension of the TD-learning algorithm for estimating the return densities in an unknown environment. As test instances, several parametric density estimation algorithms are presented for the Gaussian, Laplace, and skewed Laplace distributions. We show that these algorithms lead to risk-sensitive as well as robust RL paradigms through numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge