Parameter Identification and Motion Control for Articulated Rigid Body Robots Using Differentiable Position-based Dynamics
Paper and Code
Jan 15, 2022
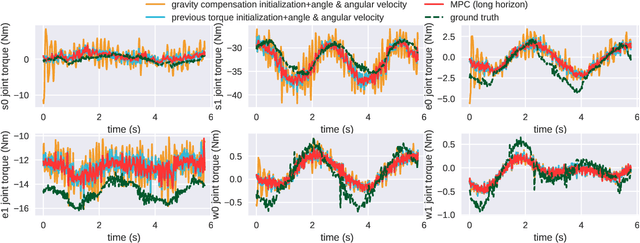
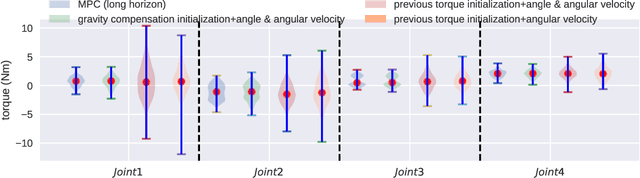
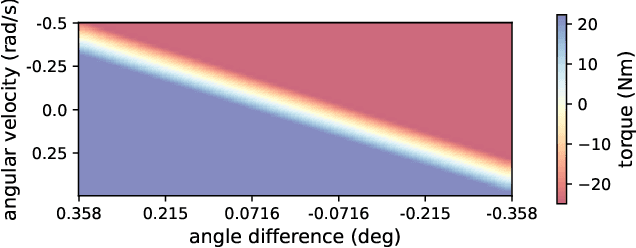
Simulation modeling of robots, objects, and environments is the backbone for all model-based control and learning. It is leveraged broadly across dynamic programming and model-predictive control, as well as data generation for imitation, transfer, and reinforcement learning. In addition to fidelity, key features of models in these control and learning contexts are speed, stability, and native differentiability. However, many popular simulation platforms for robotics today lack at least one of the features above. More recently, position-based dynamics (PBD) has become a very popular simulation tool for modeling complex scenes of rigid and non-rigid object interactions, due to its speed and stability, and is starting to gain significant interest in robotics for its potential use in model-based control and learning. Thus, in this paper, we present a mathematical formulation for coupling position-based dynamics (PBD) simulation and optimal robot design, model-based motion control and system identification. Our framework breaks down PBD definitions and derivations for various types of joint-based articulated rigid bodies. We present a back-propagation method with automatic differentiation, which can integrate both positional and angular geometric constraints. Our framework can critically provide the native gradient information and perform gradient-based optimization tasks. We also propose articulated joint model representations and simulation workflow for our differentiable framework. We demonstrate the capability of the framework in efficient optimal robot design, accurate trajectory torque estimation and supporting spring stiffness estimation, where we achieve minor errors. We also implement impedance control in real robots to demonstrate the potential of our differentiable framework in human-in-the-loop applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge