$p$-DkNN: Out-of-Distribution Detection Through Statistical Testing of Deep Representations
Paper and Code
Jul 25, 2022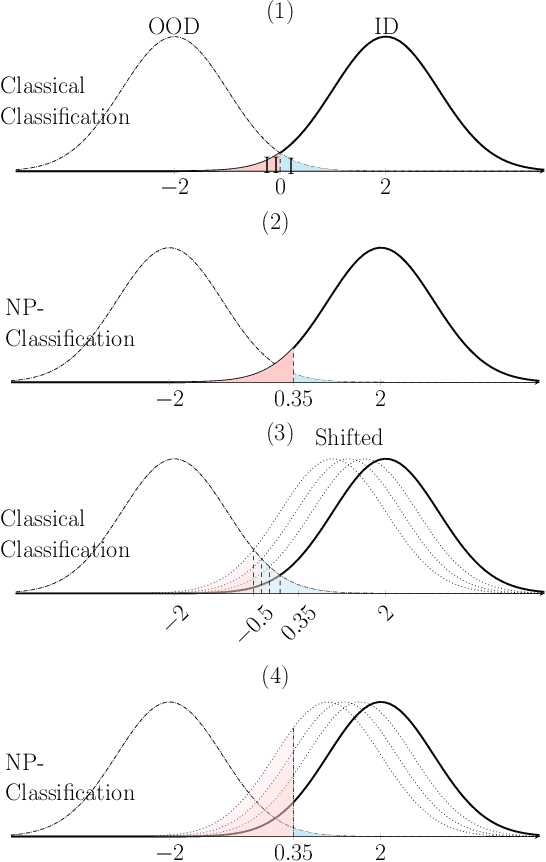
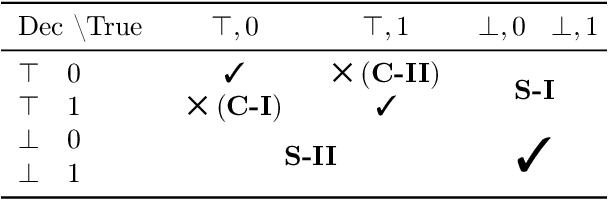
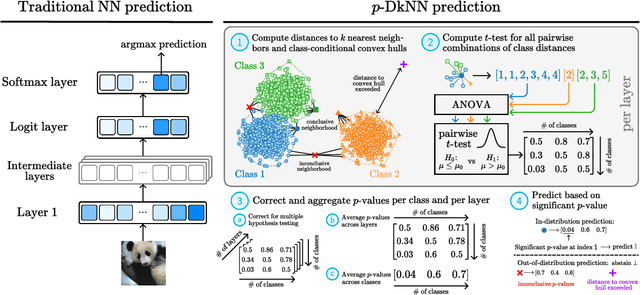
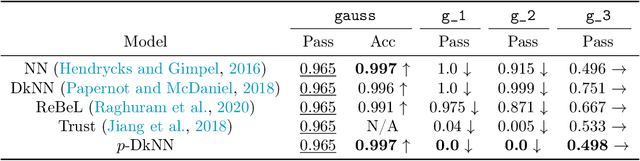
The lack of well-calibrated confidence estimates makes neural networks inadequate in safety-critical domains such as autonomous driving or healthcare. In these settings, having the ability to abstain from making a prediction on out-of-distribution (OOD) data can be as important as correctly classifying in-distribution data. We introduce $p$-DkNN, a novel inference procedure that takes a trained deep neural network and analyzes the similarity structures of its intermediate hidden representations to compute $p$-values associated with the end-to-end model prediction. The intuition is that statistical tests performed on latent representations can serve not only as a classifier, but also offer a statistically well-founded estimation of uncertainty. $p$-DkNN is scalable and leverages the composition of representations learned by hidden layers, which makes deep representation learning successful. Our theoretical analysis builds on Neyman-Pearson classification and connects it to recent advances in selective classification (reject option). We demonstrate advantageous trade-offs between abstaining from predicting on OOD inputs and maintaining high accuracy on in-distribution inputs. We find that $p$-DkNN forces adaptive attackers crafting adversarial examples, a form of worst-case OOD inputs, to introduce semantically meaningful changes to the inputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge