Output-Constrained Lossy Source Coding With Application to Rate-Distortion-Perception Theory

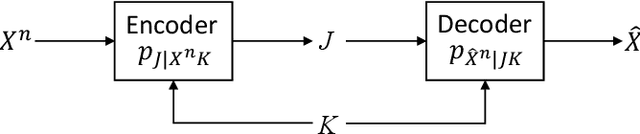
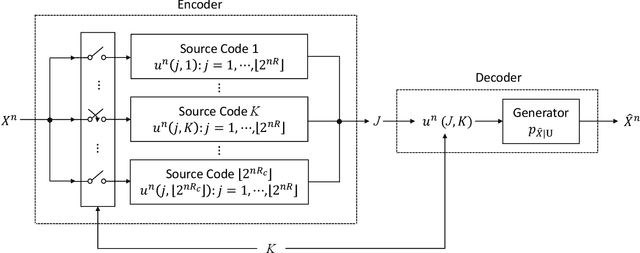
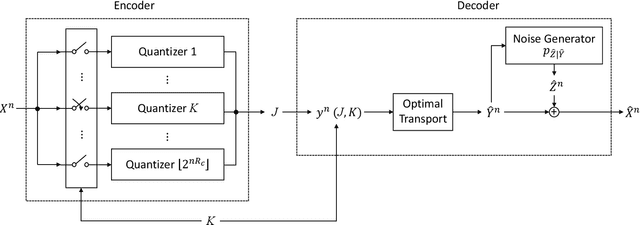
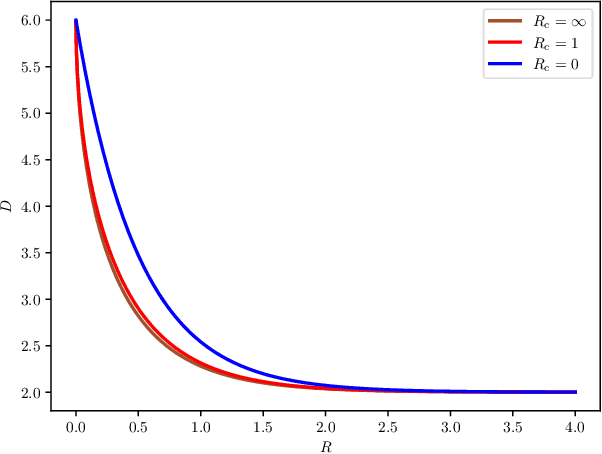
The distortion-rate function of output-constrained lossy source coding with limited common randomness is analyzed for the special case of squared error distortion measure. An explicit expression is obtained when both source and reconstruction distributions are Gaussian. This further leads to a partial characterization of the information-theoretic limit of quadratic Gaussian rate-distortion-perception coding with the perception measure given by Kullback-Leibler divergence or squared quadratic Wasserstein distance.