Out-of-Distribution Detection with Hilbert-Schmidt Independence Optimization
Paper and Code
Sep 26, 2022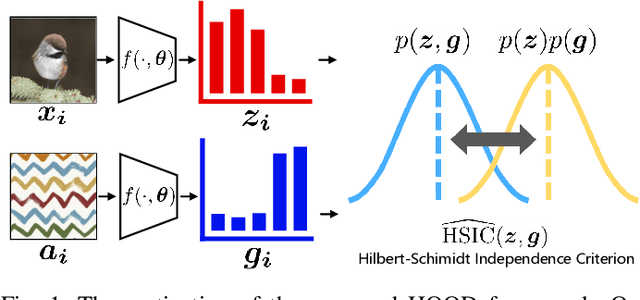
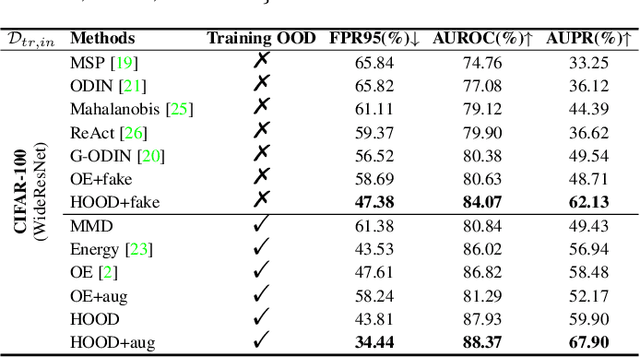
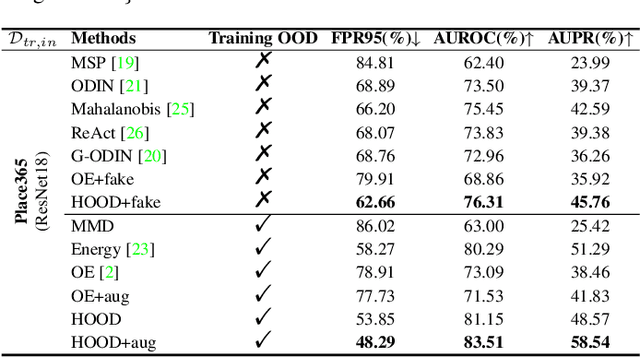
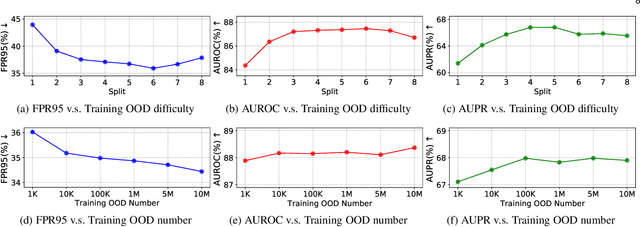
Outlier detection tasks have been playing a critical role in AI safety. There has been a great challenge to deal with this task. Observations show that deep neural network classifiers usually tend to incorrectly classify out-of-distribution (OOD) inputs into in-distribution classes with high confidence. Existing works attempt to solve the problem by explicitly imposing uncertainty on classifiers when OOD inputs are exposed to the classifier during training. In this paper, we propose an alternative probabilistic paradigm that is both practically useful and theoretically viable for the OOD detection tasks. Particularly, we impose statistical independence between inlier and outlier data during training, in order to ensure that inlier data reveals little information about OOD data to the deep estimator during training. Specifically, we estimate the statistical dependence between inlier and outlier data through the Hilbert-Schmidt Independence Criterion (HSIC), and we penalize such metric during training. We also associate our approach with a novel statistical test during the inference time coupled with our principled motivation. Empirical results show that our method is effective and robust for OOD detection on various benchmarks. In comparison to SOTA models, our approach achieves significant improvement regarding FPR95, AUROC, and AUPR metrics. Code is available: \url{https://github.com/jylins/hood}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge