Orthogonal Constrained Minimization with Tensor $\ell_{2,p}$ Regularization for HSI Denoising and Destriping

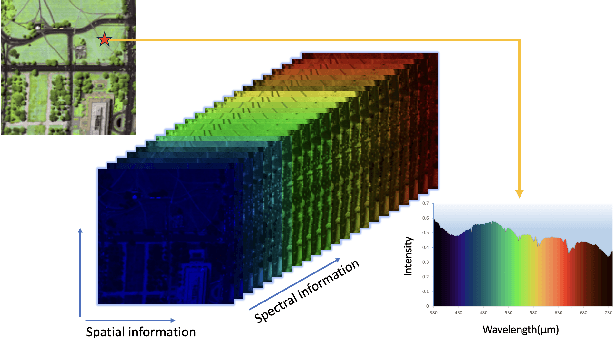
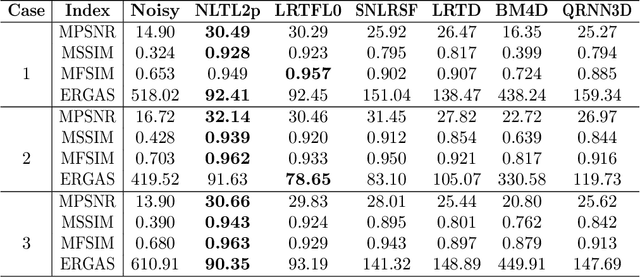
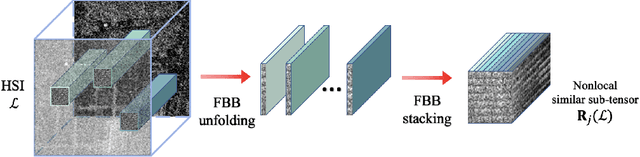
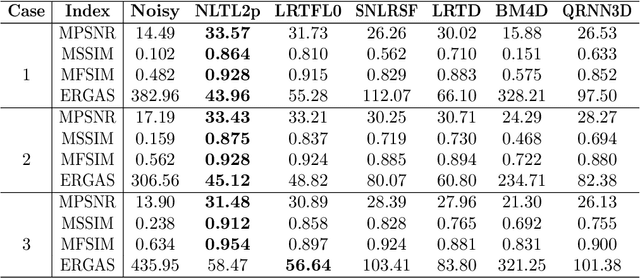
Hyperspectral images (HSIs) are often contaminated by a mixture of noises such as Gaussian noise, dead lines, stripes, and so on. In this paper, we propose a novel approach for HSI denoising and destriping, called NLTL2p, which consists of an orthogonal constrained minimization model and an iterative algorithm with convergence guarantees. The model of the proposed NLTL2p approach is built based on a new sparsity-enhanced Nonlocal Low-rank Tensor regularization and a tensor $\ell_{2,p}$ norm with $p\in(0,1)$. The low-rank constraints for HSI denoising utilize the spatial nonlocal self-similarity and spectral correlation of HSIs and are formulated based on independent higher-order singular value decomposition with sparsity enhancement on its core tensor to prompt more low-rankness. The tensor $\ell_{2,p}$ norm for HSI destriping is extended from the matrix $\ell_{2,p}$ norm. A proximal block coordinate descent algorithm is proposed in the NLTL2p approach to solve the resulting nonconvex nonsmooth minimization with orthogonal constraints. We show any accumulation point of the sequence generated by the proposed algorithm converges to a first-order stationary point, which is defined using three equalities of substationarity, symmetry, and feasibility for orthogonal constraints. In the numerical experiments, we compare the proposed method with state-of-the-art methods including a deep learning based method, and test the methods on both simulated and real HSI datasets. Our proposed NLTL2p method demonstrates outperformance in terms of metrics such as mean peak signal-to-noise ratio as well as visual quality.