Optimal Tourist Problem and Anytime Planning of Trip Itineraries
Paper and Code
Oct 08, 2014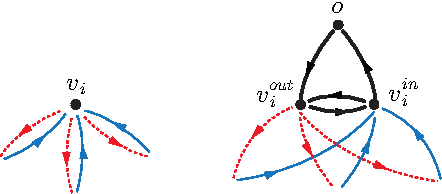
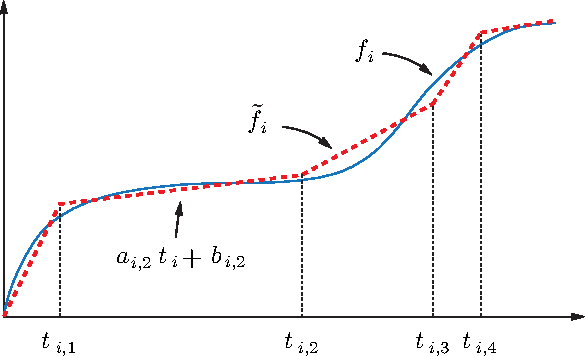
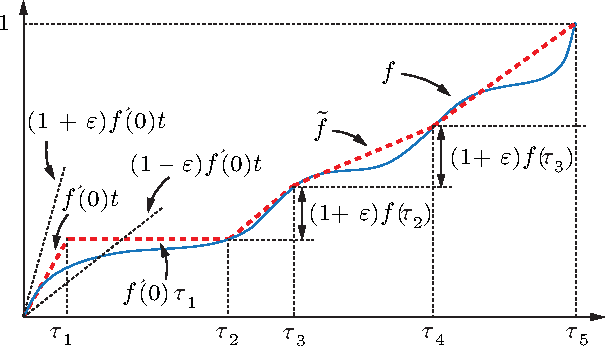
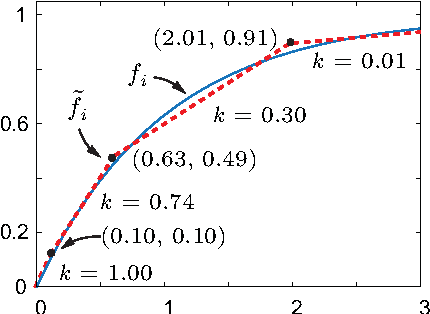
We introduce and study the problem in which a mobile sensing robot (our tourist) is tasked to travel among and gather intelligence at a set of spatially distributed point-of-interests (POIs). The quality of the information collected at each POI is characterized by some non-decreasing reward function over the time spent at the POI. With limited time budget, the robot must balance between spending time traveling to POIs and spending time at POIs for information collection (sensing) so as to maximize the total reward. Alternatively, the robot may be required to acquire a minimum mount of reward and hopes to do so with the least amount of time. We propose a mixed integer programming (MIP) based anytime algorithm for solving these two NP-hard optimization problems to arbitrary precision. The effectiveness of our algorithm is demonstrated using an extensive set of computational experiments including the planning of a realistic itinerary for a first-time tourist in Istanbul.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge