Optimal Baseline Corrections for Off-Policy Contextual Bandits
Paper and Code
May 09, 2024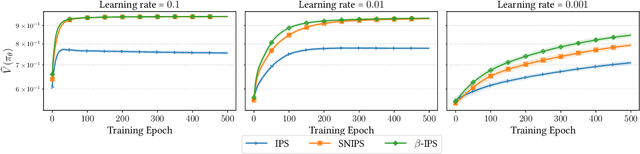
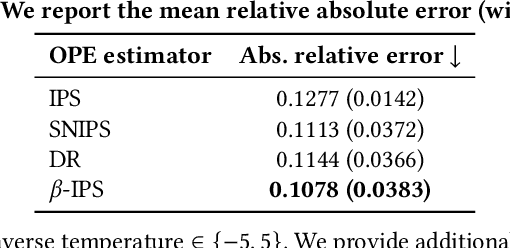
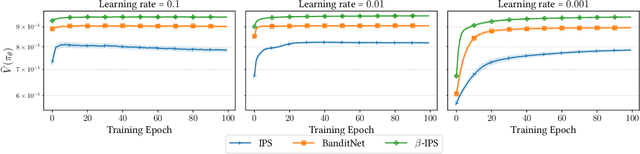
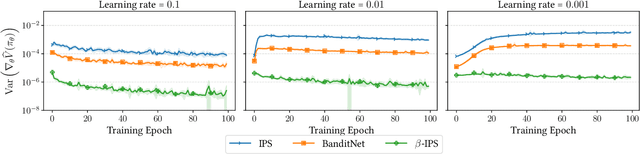
The off-policy learning paradigm allows for recommender systems and general ranking applications to be framed as decision-making problems, where we aim to learn decision policies that optimize an unbiased offline estimate of an online reward metric. With unbiasedness comes potentially high variance, and prevalent methods exist to reduce estimation variance. These methods typically make use of control variates, either additive (i.e., baseline corrections or doubly robust methods) or multiplicative (i.e., self-normalisation). Our work unifies these approaches by proposing a single framework built on their equivalence in learning scenarios. The foundation of our framework is the derivation of an equivalent baseline correction for all of the existing control variates. Consequently, our framework enables us to characterize the variance-optimal unbiased estimator and provide a closed-form solution for it. This optimal estimator brings significantly improved performance in both evaluation and learning, and minimizes data requirements. Empirical observations corroborate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge