On the Sample Complexity of Rank Regression from Pairwise Comparisons
Paper and Code
May 04, 2021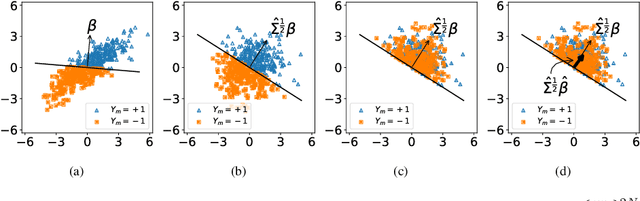

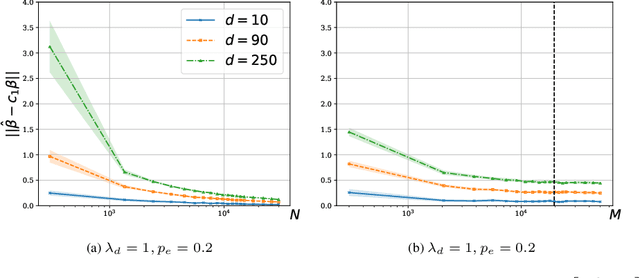
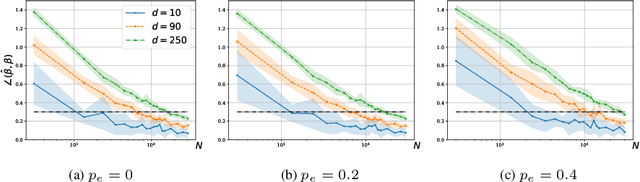
We consider a rank regression setting, in which a dataset of $N$ samples with features in $\mathbb{R}^d$ is ranked by an oracle via $M$ pairwise comparisons. Specifically, there exists a latent total ordering of the samples; when presented with a pair of samples, a noisy oracle identifies the one ranked higher with respect to the underlying total ordering. A learner observes a dataset of such comparisons and wishes to regress sample ranks from their features. We show that to learn the model parameters with $\epsilon > 0$ accuracy, it suffices to conduct $M \in \Omega(dN\log^3 N/\epsilon^2)$ comparisons uniformly at random when $N$ is $\Omega(d/\epsilon^2)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge