On the $f$-Differential Privacy Guarantees of Discrete-Valued Mechanisms
Paper and Code
Feb 19, 2023
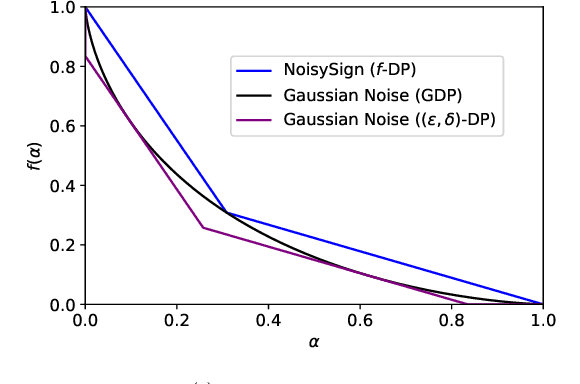
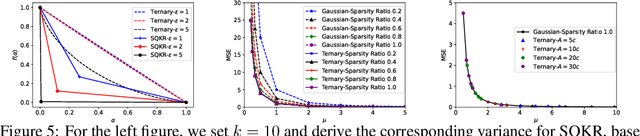
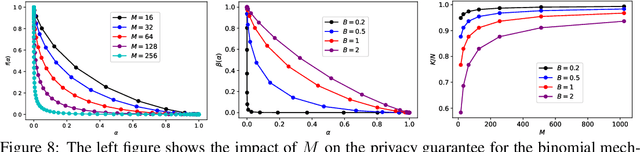
We consider a federated data analytics problem in which a server coordinates the collaborative data analysis of multiple users with privacy concerns and limited communication capability. The commonly adopted compression schemes introduce information loss into local data while improving communication efficiency, and it remains an open question whether such discrete-valued mechanisms provide any privacy protection. Considering that differential privacy has become the gold standard for privacy measures due to its simple implementation and rigorous theoretical foundation, in this paper, we study the privacy guarantees of discrete-valued mechanisms with finite output space in the lens of $f$-differential privacy (DP). By interpreting the privacy leakage as a hypothesis testing problem, we derive the closed-form expression of the tradeoff between type I and type II error rates, based on which the $f$-DP guarantees of a variety of discrete-valued mechanisms, including binomial mechanisms, sign-based methods, and ternary-based compressors, are characterized. We further investigate the Byzantine resilience of binomial mechanisms and ternary compressors and characterize the tradeoff among differential privacy, Byzantine resilience, and communication efficiency. Finally, we discuss the application of the proposed method to differentially private stochastic gradient descent in federated learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge