On Scalable Variant of Wasserstein Barycenter
Paper and Code
Oct 10, 2019
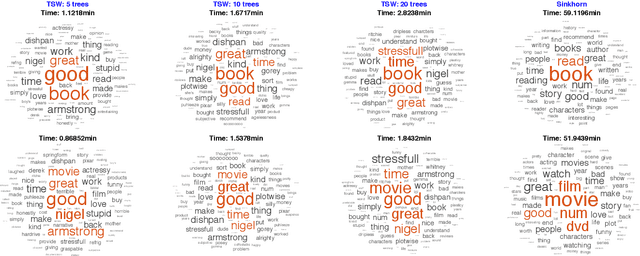
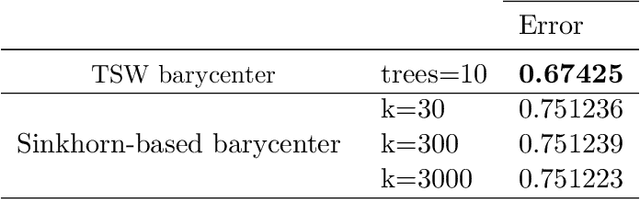
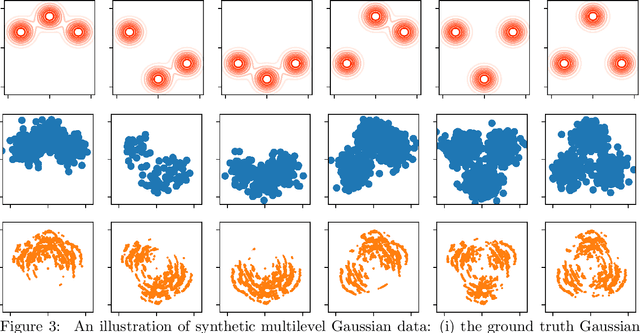
We study a variant of Wasserstein barycenter problem, which we refer to as \emph{tree-sliced Wasserstein barycenter}, by leveraging the structure of tree metrics for the ground metrics in the formulation of Wasserstein distance. Drawing on the tree structure, we propose efficient algorithms for solving the unconstrained and constrained versions of tree-sliced Wasserstein barycenter. The algorithms have fast computational time and efficient memory usage, especially for high dimensional settings while demonstrating favorable results when the tree metrics are appropriately constructed. Experimental results on large-scale synthetic and real datasets from Wasserstein barycenter for documents with word embedding, multilevel clustering, and scalable Bayes problems show the advantages of tree-sliced Wasserstein barycenter over (Sinkhorn) Wasserstein barycenter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge