On Learning to Rank Long Sequences with Contextual Bandits
Paper and Code
Jun 07, 2021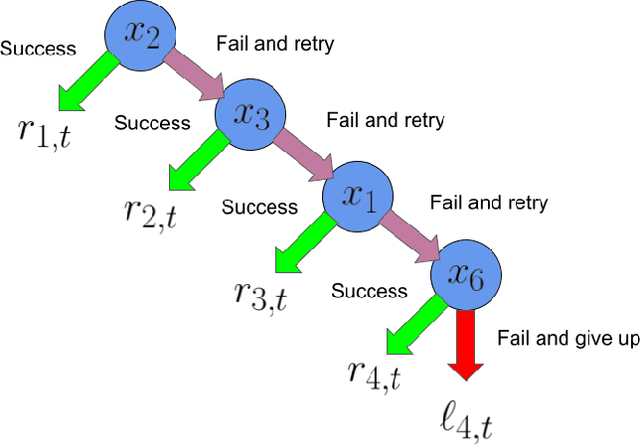
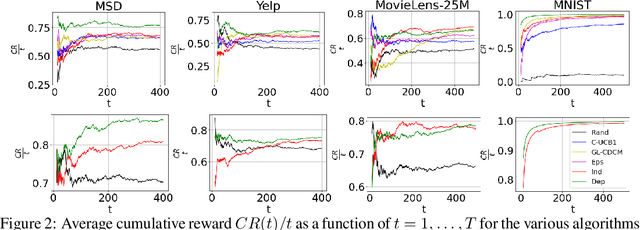
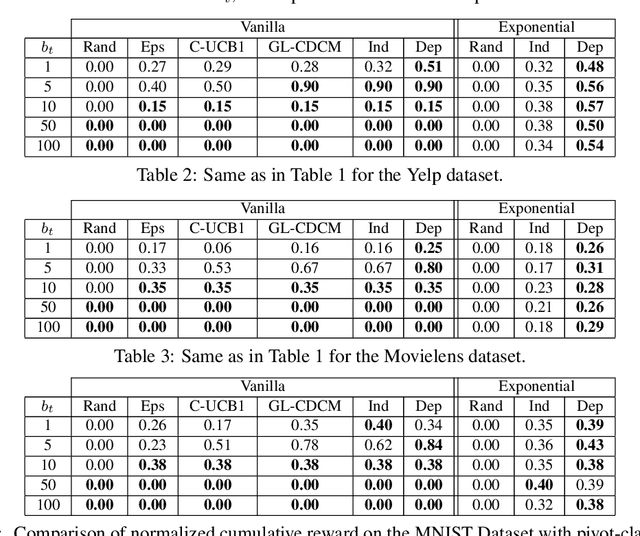
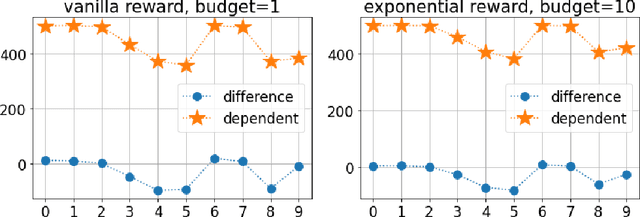
Motivated by problems of learning to rank long item sequences, we introduce a variant of the cascading bandit model that considers flexible length sequences with varying rewards and losses. We formulate two generative models for this problem within the generalized linear setting, and design and analyze upper confidence algorithms for it. Our analysis delivers tight regret bounds which, when specialized to vanilla cascading bandits, results in sharper guarantees than previously available in the literature. We evaluate our algorithms on a number of real-world datasets, and show significantly improved empirical performance as compared to known cascading bandit baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge