On Diffusion Process in SE-invariant Space

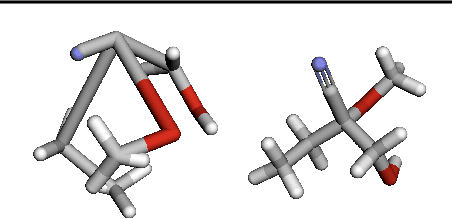
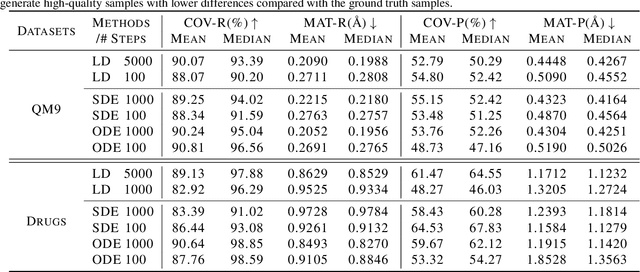
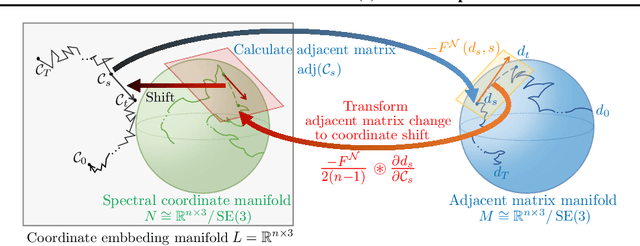
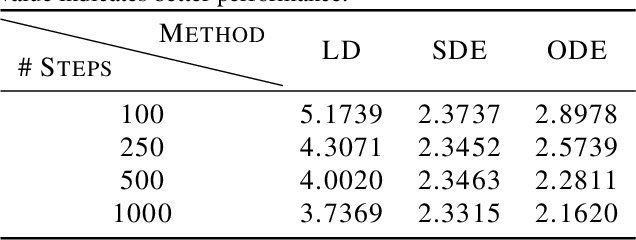
Sampling viable 3D structures (e.g., molecules and point clouds) with SE(3)-invariance using diffusion-based models proved promising in a variety of real-world applications, wherein SE(3)-invariant properties can be naturally characterized by the inter-point distance manifold. However, due to the non-trivial geometry, we still lack a comprehensive understanding of the diffusion mechanism within such SE(3)-invariant space. This study addresses this gap by mathematically delineating the diffusion mechanism under SE(3)-invariance, via zooming into the interaction behavior between coordinates and the inter-point distance manifold through the lens of differential geometry. Upon this analysis, we propose accurate and projection-free diffusion SDE and ODE accordingly. Such formulations enable enhancing the performance and the speed of generation pathways; meanwhile offering valuable insights into other systems incorporating SE(3)-invariance.