Normalized Direction-preserving Adam
Paper and Code
Sep 18, 2018

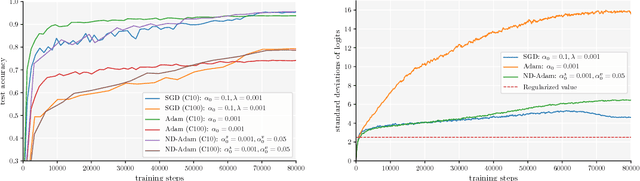
Adaptive optimization algorithms, such as Adam and RMSprop, have shown better optimization performance than stochastic gradient descent (SGD) in some scenarios. However, recent studies show that they often lead to worse generalization performance than SGD, especially for training deep neural networks (DNNs). In this work, we identify the reasons that Adam generalizes worse than SGD, and develop a variant of Adam to eliminate the generalization gap. The proposed method, normalized direction-preserving Adam (ND-Adam), enables more precise control of the direction and step size for updating weight vectors, leading to significantly improved generalization performance. Following a similar rationale, we further improve the generalization performance in classification tasks by regularizing the softmax logits. By bridging the gap between SGD and Adam, we also hope to shed light on why certain optimization algorithms generalize better than others.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge