Non-Parametric Stochastic Sequential Assignment With Random Arrival Times
Paper and Code
Jun 09, 2021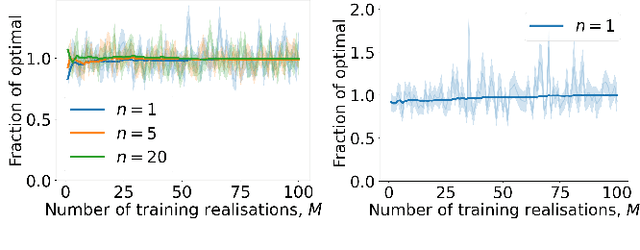

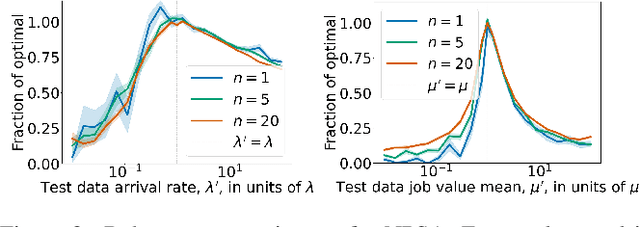

We consider a problem wherein jobs arrive at random times and assume random values. Upon each job arrival, the decision-maker must decide immediately whether or not to accept the job and gain the value on offer as a reward, with the constraint that they may only accept at most $n$ jobs over some reference time period. The decision-maker only has access to $M$ independent realisations of the job arrival process. We propose an algorithm, Non-Parametric Sequential Allocation (NPSA), for solving this problem. Moreover, we prove that the expected reward returned by the NPSA algorithm converges in probability to optimality as $M$ grows large. We demonstrate the effectiveness of the algorithm empirically on synthetic data and on public fraud-detection datasets, from where the motivation for this work is derived.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge