Node-oriented Spectral Filtering for Graph Neural Networks

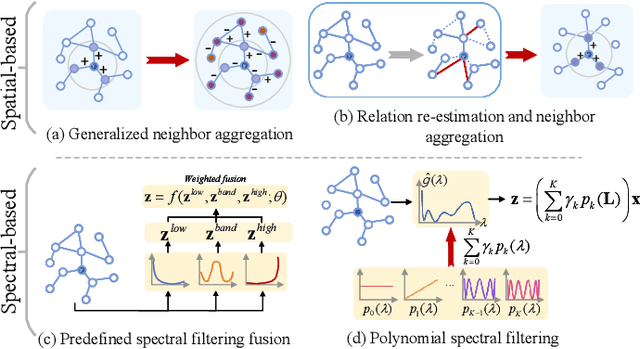
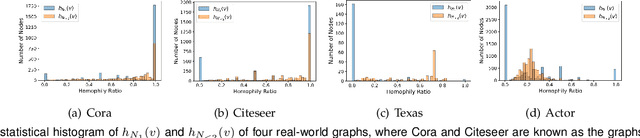
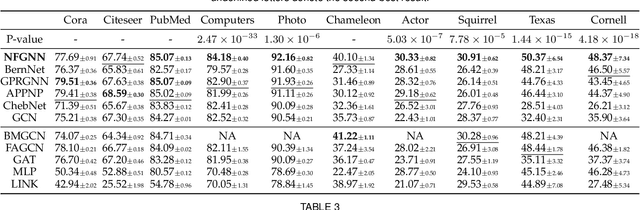
Graph neural networks (GNNs) have shown remarkable performance on homophilic graph data while being far less impressive when handling non-homophilic graph data due to the inherent low-pass filtering property of GNNs. In general, since the real-world graphs are often a complex mixture of diverse subgraph patterns, learning a universal spectral filter on the graph from the global perspective as in most current works may still suffer from great difficulty in adapting to the variation of local patterns. On the basis of the theoretical analysis on local patterns, we rethink the existing spectral filtering methods and propose the \textbf{\underline{N}}ode-oriented spectral \textbf{\underline{F}}iltering for \textbf{\underline{G}}raph \textbf{\underline{N}}eural \textbf{\underline{N}}etwork (namely NFGNN). By estimating the node-oriented spectral filter for each node, NFGNN is provided with the capability of precise local node positioning via the generalized translated operator, thus discriminating the variations of local homophily patterns adaptively. Meanwhile, the utilization of re-parameterization brings a good trade-off between global consistency and local sensibility for learning the node-oriented spectral filters. Furthermore, we theoretically analyze the localization property of NFGNN, demonstrating that the signal after adaptive filtering is still positioned around the corresponding node. Extensive experimental results demonstrate that the proposed NFGNN achieves more favorable performance.