Neural Collapse in Multi-label Learning with Pick-all-label Loss

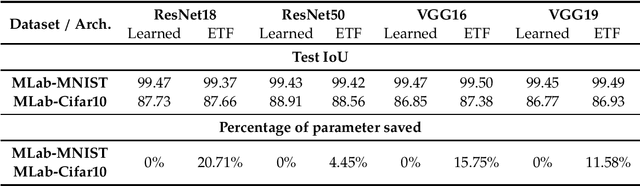
We study deep neural networks for the multi-label classification (MLab) task through the lens of neural collapse (NC). Previous works have been restricted to the multi-class classification setting and discovered a prevalent NC phenomenon comprising of the following properties for the last-layer features: (i) the variability of features within every class collapses to zero, (ii) the set of feature means form an equi-angular tight frame (ETF), and (iii) the last layer classifiers collapse to the feature mean upon some scaling. We generalize the study to multi-label learning, and prove for the first time that a generalized NC phenomenon holds with the "pick-all-label" formulation. Under the natural analog of the unconstrained feature model (UFM), we establish that the only global classifier of the pick-all-label cross entropy loss display the same ETF geometry which further collapse to multiplicity-1 feature class means. Besides, we discover a combinatorial property in generalized NC which is unique for multi-label learning that we call "tag-wise average" property, where the feature class-means of samples with multiple labels are scaled average of the feature class-means of single label tags. Theoretically, we establish global optimality result for the pick-all-label cross-entropy risk for the UFM. Additionally, We also provide empirical evidence to support our investigation into training deep neural networks on multi-label datasets, resulting in improved training efficiency.