Near-Optimal Multi-Agent Learning for Safe Coverage Control
Paper and Code
Oct 12, 2022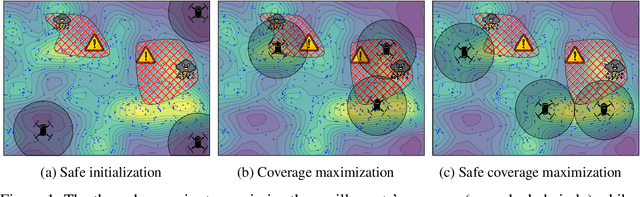
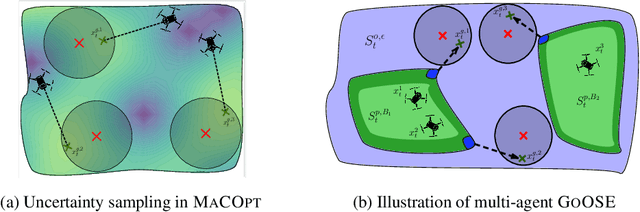
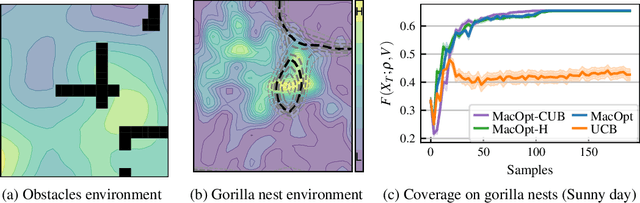
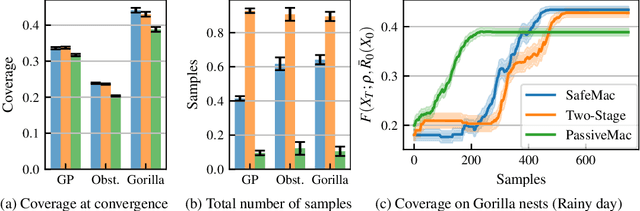
In multi-agent coverage control problems, agents navigate their environment to reach locations that maximize the coverage of some density. In practice, the density is rarely known $\textit{a priori}$, further complicating the original NP-hard problem. Moreover, in many applications, agents cannot visit arbitrary locations due to $\textit{a priori}$ unknown safety constraints. In this paper, we aim to efficiently learn the density to approximately solve the coverage problem while preserving the agents' safety. We first propose a conditionally linear submodular coverage function that facilitates theoretical analysis. Utilizing this structure, we develop MacOpt, a novel algorithm that efficiently trades off the exploration-exploitation dilemma due to partial observability, and show that it achieves sublinear regret. Next, we extend results on single-agent safe exploration to our multi-agent setting and propose SafeMac for safe coverage and exploration. We analyze SafeMac and give first of its kind results: near optimal coverage in finite time while provably guaranteeing safety. We extensively evaluate our algorithms on synthetic and real problems, including a bio-diversity monitoring task under safety constraints, where SafeMac outperforms competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge