NDGGNET-A Node Independent Gate based Graph Neural Networks
Paper and Code
May 11, 2022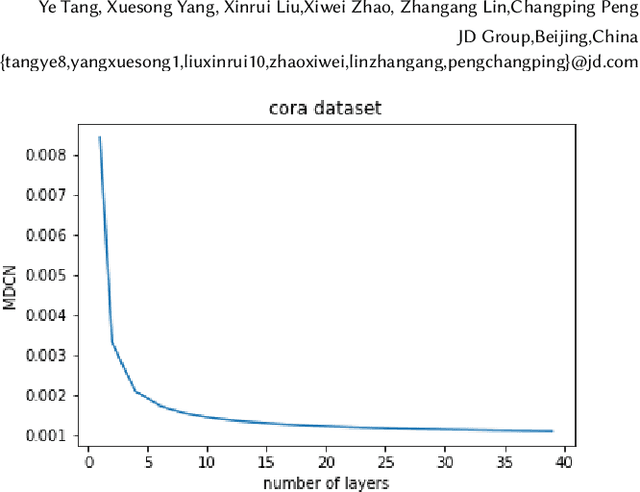

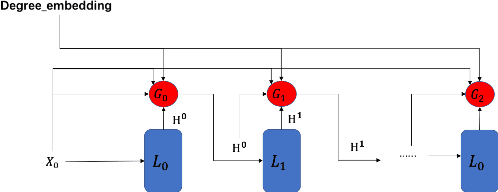

Graph Neural Networks (GNNs) is an architecture for structural data, and has been adopted in a mass of tasks and achieved fabulous results, such as link prediction, node classification, graph classification and so on. Generally, for a certain node in a given graph, a traditional GNN layer can be regarded as an aggregation from one-hop neighbors, thus a set of stacked layers are able to fetch and update node status within multi-hops. For nodes with sparse connectivity, it is difficult to obtain enough information through a single GNN layer as not only there are only few nodes directly connected to them but also can not propagate the high-order neighbor information. However, as the number of layer increases, the GNN model is prone to over-smooth for nodes with the dense connectivity, which resulting in the decrease of accuracy. To tackle this issue, in this thesis, we define a novel framework that allows the normal GNN model to accommodate more layers. Specifically, a node-degree based gate is employed to adjust weight of layers dynamically, that try to enhance the information aggregation ability and reduce the probability of over-smoothing. Experimental results show that our proposed model can effectively increase the model depth and perform well on several datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge